Gọi (a ) là số thực lớn nhất để bất phương trình ({x^2} - x + 2 + a ln left( {{x^2} - x + 1} right) ge 0 ) nghiệm đúng với mọi (x in mathbb{R}. ) Mệnh đề nào sau đây đúng?

* Hướng dẫn giải

Với \(a = 0\) có \({x^2} - x + 2 + a\ln \left( {{x^2} - x + 1} \right) \ge 0 \Leftrightarrow {x^2} - x + 2 \ge 0,\forall x \in \mathbb{R}\) suy ra \(a = 0\) thỏa mãn.

Vậy ta chỉ cần tìm các giá trị \(a >0.\)

Đặt \(t = {x^2} - x + 1,\) có \(t \ge \frac{3}{4}.\)

Bất phương trình đưa về tìm \(a >0\) để \(t + 1 + a\ln t \ge 0,\forall t \ge \frac{3}{4}.\)

Đặt \(f\left( t \right) = t + 1 + a\ln t\) có \(f'\left( t \right) = 1 + \frac{a}{t} >0,\forall a >0,t \ge \frac{3}{4}.\)

Bảng biến thiên

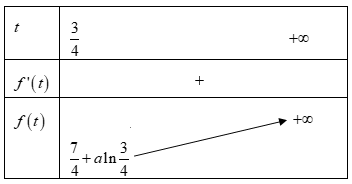
Có \(f\left( t \right) \ge 0,\forall t \ge \frac{3}{4}\) khi và chỉ khi \(\frac{7}{4} + a\ln \frac{3}{4} \ge 0 \Leftrightarrow a \le \frac{{ - 7}}{{4\ln \frac{3}{4}}} \approx 6,08 \Rightarrow a \in \left( {6;7} \right].\)

Đáp án A