Một mặt cầu tâm (O ) nằm trên mặt phẳng đáy của hình chóp tam giác đều (S.ABC ) có tất cả các cạnh bằng nhau, các đỉnh (A,B,C ) thuộc mặt cầu. Biết bán kính mặt cầu là 1. Tính tổng...

* Hướng dẫn giải

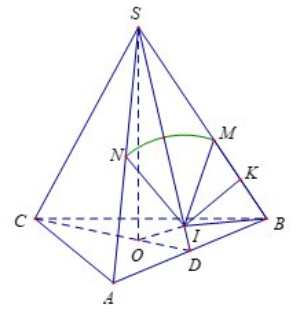
Gọi \(D\) là trung điểm của đoạn \(AB,\) kẻ \(OI \bot SD,\) dễ dàng chứng minh được \(OI \bot \left( {SAB} \right).\)

Suy ra \(I\) là tâm đường tròn \(\left( C \right)\) giao tuyến của mặt cầu tâm \(O\) với mặt phẳng \(\left( {SAB} \right).\) Gọi \(M,N\) lần lượt là giao điểm của đường tròn \(\left( C \right)\) với \(SB,SA;K\) là trung điểm của \(MB.\)

Giả sử \(AB = a,\) theo giả thiết ta suy ra \(OC = 1 \Leftrightarrow \frac{{a\sqrt 3 }}{2} = 1 \Leftrightarrow a = \sqrt 3 .\)

Ta có \(SD = CD = \frac{3}{2},OD = \frac{1}{2},SO = \sqrt {S{C^2} - O{C^2}} = \sqrt 2 ,OI = \frac{{SO.OD}}{{SD}} = \frac{{\sqrt 2 }}{3},\) \(ID = \frac{{O{D^2}}}{{SD}} = \frac{1}{6},SI = \frac{4}{3}.\)

Gọi \(r\) là bán kính đường tròn \(\left( C \right),\) khi đó \(r = \sqrt {1 - O{I^2}} = \frac{{\sqrt 7 }}{3}.\)

Ta có tam giác \(SIK\) vuông tại \(K\) và góc \(\angle ISK = {30^0}\) suy ra \(IK = \frac{1}{2}IS = \frac{2}{3}\)

Xét tam giác \(MIK\) có \(\cos I = \frac{{IK}}{{IM}} = \frac{2}{{\sqrt 7 }} \Rightarrow I \approx {28^0} \Rightarrow \angle MIN \approx {64^0}\)

Khi đó chiều dài cung \(MN\) bằng \(\frac{{64}}{{180}}.\frac{{\sqrt 7 }}{3} = \frac{{16\sqrt 7 }}{{135}}.\) Vậy tổng độ dài \(l,\) các giao tuyến của mặt cầu với các mặt bên của hình chóp là \(l = \frac{{16\sqrt 7 }}{{45}} \approx 0,94.\)

Đáp án D