Cho hình nón đỉnh S, đường cao SO,A và B là hai điểm thuộc đường tròn đáy sao cho khoảng cách từ O đến mặt phẳng

* Hướng dẫn giải

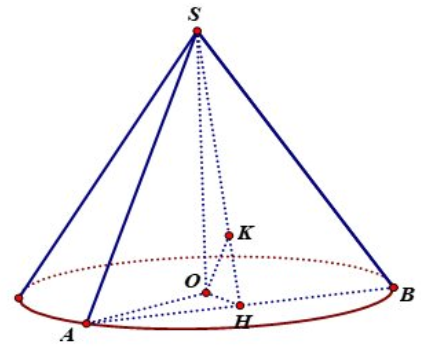
Gọi \(H\) là trung điểm của \(AB.\)

Tam giác \(OAB\) là tam giác cân nên \(OH \bot AB\)

Mặt khác \(SO \bot AB\) nên \(AB \bot \left( {SOH} \right)\) do đó \(\left( {SOH} \right) \bot \left( {SAB} \right)\) theo giao tuyến \(SH\)

Từ \(O\) kẻ \(OK \bot SH\) suy ra \(OK \bot \left( {SAB} \right) \Rightarrow d\left( {O;\left( {SAB} \right)} \right) = OK\)

Tam giác \(SAB\) là tam giác cân tại \(S\) (vì \(SA = SB)\)

Lại có \(\widehat {SAB} = {60^0}\) nên tam giác \(SAB\) là tam giác đều

Đặt \(SA = SB = AB = 2x;OA = r\)

Trong tam giác vuông \(SOA\) có \(SO = OA.\tan \widehat {SAO} = \frac{r}{{\sqrt 3 }}\)

Trong tam giác vuông \(SOH\) có \(OH = \sqrt {O{A^2} - A{H^2}} = \sqrt {{r^2} - {x^2}} \)

Trong tam giác đều \(SAB\) có \(SH = \frac{{AB\sqrt 3 }}{2} = x\sqrt 3 \)

Ta có \(S{H^2} = S{O^2} + O{H^2} \Leftrightarrow 3{x^2} = \frac{{{r^2}}}{3} + {r^2} - {x^2} \Leftrightarrow r = x\sqrt 3 \)

Trong tam giác vuông \(SOH\) có \(\frac{1}{{O{K^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{H^2}}} \Leftrightarrow \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}}} = \frac{1}{{{{\left( {\frac{r}{{\sqrt 3 }}} \right)}^2}}} + \frac{1}{{{r^2} - {x^2}}}\)

\( \Leftrightarrow \frac{3}{{{a^2}}} = \frac{1}{{{x^2}}} + \frac{1}{{2{x^2}}} \Leftrightarrow x = \frac{{a\sqrt 2 }}{2}\)

Vậy độ dài đường sinh của hình nón là \(l = SA = 2x = a\sqrt 2 .\)

Đáp án D