Cho lăng trụ đứng ABC.A'B'C' có độ dài cạnh bên là 2a, đáy ABC là tam giác vuông cân tại A, góc giữa AC' và mặt phẳng
Câu hỏi :
Cho lăng trụ đứng \(ABC.A'B'C'\) có độ dài cạnh bên là \(2a,\) đáy \(ABC\) là tam giác vuông cân tại \(A,\) góc giữa \(AC'\) và mặt phẳng \(\left( {BCC'B'} \right)\) bằng \({30^0}\) (tham khảo hình vẽ).
A.\(\pi {a^3}.\)
B. \(3\pi {a^3}.\)
C.\(2\pi {a^3}.\)
D.\(4\pi {a^3}.\)
* Đáp án
D
* Hướng dẫn giải
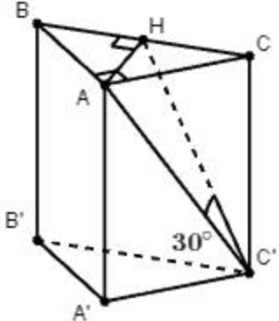
Gọi \(H\) là trung điểm của đoạn \(BC,\) vì \(\Delta ABC\) là tam giác vuông cân nên \(H\) là chân đường cao xuất phát từ đỉnh \(A\) đồng thời cũng là tâm đường tròn ngoại tiếp \(\Delta ABC.\)
Suy ra bán kính đường tròn ngoại tiếp đáy của lăng trụ \(ABC.A'B'C'\) là \(HC.\)
Vì \(\left\{ \begin{array}{l}AH \bot BC\\AH \bot BB'\end{array} \right.\) nên \(AH \bot \left( {BCC'B'} \right).\)
Suy ra \(HC\) là hình chiếu vuông góc của \(AC\) lên \(\left( {BCC'B'} \right).\)
Góc giữa \(AC'\) và mặt phẳng \(\left( {BCC'B'} \right)\) là \(\widehat {AC'H} = {30^0}.\)
Đặt \(HC = x \Rightarrow AC = x\sqrt 2 .\)
Áp dụng định lý Pytago trong \(\Delta ACC'\) ta được \(AC' = \sqrt {2{x^2} + 4{a^2}} .\)
Áp dụng định lý Pytago trong \(\Delta HCC'\) ta được \[HC' = \sqrt {{x^2} + 4{a^2}} .\]
Xét \(\Delta AHC'\) vuông tại \(H\) có: \(\cos \left( {{{30}^0}} \right) = \frac{{HC'}}{{AC'}} \Leftrightarrow \frac{{\sqrt 3 }}{2} = \sqrt {\frac{{{x^2} + 4{a^2}}}{{2{x^2} + 4{a^2}}}} .\)
Khi đó: \(\frac{3}{4} = \frac{{{x^2} + 4{a^2}}}{{2{x^2} + 4{a^2}}} \Leftrightarrow 6{x^2} + 12{a^2} = 4{x^2} + 16{a^2} \Leftrightarrow x = a\sqrt 2 .\)
Thể tích khối trụ có hai đáy là hai đường tròn ngoại tiếp của lăng trụ \(ABC.A'B'C'\) là:
\(V = \pi {R^2}h = \pi {\left( {HC} \right)^2}CC' = \pi {\left( {a\sqrt 2 } \right)^2}.2a = 4\pi {a^3}.\)
Đáp án D
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề) !!
Copyright © 2021 HOCTAP247
