Cho hình chóp đều S.ABCD cạnh đáy bằng a, d(a;(ABCD))=(a căn 3)/2 . Góc giữa mặt phẳng (SBC) và mặt phẳng

* Hướng dẫn giải

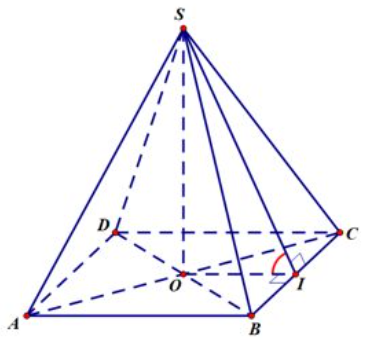
Hình chóp \(S.ABCD\) là chóp đều nên gọi \(O\) là tâm của hình vuông \(ABCD\) ta suy ra \(SO \bot \left( {ABCD} \right),\) do đó \(d\left( {S,\left( {ABCD} \right)} \right) = SO\) hay ta có \(SO = \frac{{a\sqrt 3 }}{2}.\)

Gọi \(I\) là trung điểm của \(BC\) ta có \(\left\{ \begin{array}{l}OI \bot BC\\SI \bot BC\end{array} \right.\) suy ra góc giữa mặt phẳng \(\left( {SBC} \right)\) và mặt phẳng \(\left( {ABCD} \right)\) là góc \(\widehat {SIO}.\)

Ta có \(\tan \widehat {SIO} = \frac{{SO}}{{IO}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{\frac{a}{2}}} = \sqrt 3 ,\) do vậy \(\widehat {SIO} = {60^0}.\)

Vậy góc giữa mặt phẳng \(\left( {SBC} \right)\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({60^0}.\)

Đáp án A