Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật AB = a;AD = 4a;SA = a căn 15 ,SA vuông góc ABCD

* Hướng dẫn giải

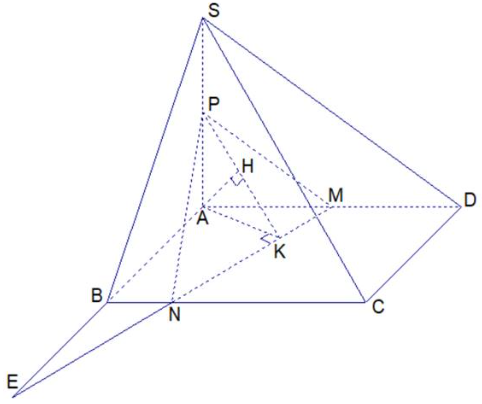
Gọi \(P\) là trung điểm \(SA.\) Ta có \(SD//MP \Rightarrow SD//\left( {MNP} \right)\)

Do đó \(d\left( {SD,MN} \right) = d\left( {SD,\left( {MNP} \right)} \right) = d\left( {D,\left( {MNP} \right)} \right) = d\left( {A,\left( {MNP} \right)} \right)\) (vì \(M\) là trung điểm \(AD).\)

Trong mặt phẳng \(\left( {ABCD} \right)\) kẻ \(AK \bot MN\) và trong mặt phẳng \(\left( {AKP} \right)\) kẻ \(AH \bot PK\)

Suy ra \(d\left( {A,\left( {MNP} \right)} \right) = AH\)

Ta có \(AP = \frac{{SA}}{2} = \frac{{a\sqrt {15} }}{2}\)

Gọi \(E = MN \cap AB \Rightarrow AE = 2a.\)

\(\Delta AME\) vuông tại \(A \Rightarrow \frac{1}{{A{K^2}}} = \frac{1}{{A{M^2}}} + \frac{1}{{A{E^2}}} = \frac{1}{{4{a^2}}} + \frac{1}{{4{a^2}}} = \frac{1}{{2{a^2}}}\)

\(\Delta AKP\) vuông tại \[\]

Vậy \(d\left( {SD,MN} \right) = \frac{{\sqrt {690} a}}{{23}}.\)

Đáp án D