Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng 3a. Gọi M thuộc cạnh B'C' sao cho MC' = 2MB'

* Hướng dẫn giải

Cách 1.

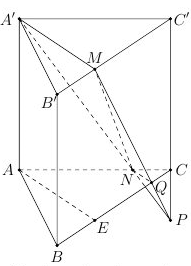
Mặt phẳng

\(\left( {A'MN} \right)\) cắt các mặt phẳng \(\left( {ABC} \right)\) và \(\left( {A'B'C'} \right)\) theo các giao tuyến song song nên \(Q\) là giao điểm của đường thẳng qua \(N\) song song với \(A'M\) với cạnh \(BC.\)

Kéo dài các đường \(A'N,MQ\) và \(C'C\) đồng quy tại cùng một điểm \(P\) (3 mặt phẳng cắt nhau theo 3 giao tuyến đồng quy).

Như vậy khối đa diện cần tính thể tích là một khối chóp cụt.

Ta có \(C'M = \frac{2}{3}B'C' = 2a.{S_1} = {S_{\Delta A'C'M}} = \frac{1}{2}A'C'.C'M.\sin {60^0} = \frac{1}{2}.3a.2a.\frac{{\sqrt 3 }}{2} = \frac{{3\sqrt 3 {a^2}}}{2}.\)

Gọi \(E\) là điểm trên cạnh \(BC\) sao cho \(EC = 2EB\) thì \(A'M//AE\) nên

 

Diện tích tam giác \(CNQ\) là \({S_2} = {S_{\Delta CNQ}} = \frac{1}{2}CQ.CN.\sin {60^0} = \frac{1}{2}.\frac{a}{2}.\frac{{3a}}{4}.\frac{{\sqrt 3 }}{2} = \frac{{3\sqrt 3 {a^2}}}{{32}}.\)

Vậy ..

Cách 2:

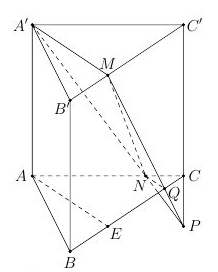
Mặt phẳng \(\left( {A'MN} \right)\) cắt các mặt phẳng \(\left( {ABC} \right)\) và \(\left( {A'B'C'} \right)\) theo các giao tuyến song song nên \(Q\) là giao điểm của đường thẳng qua \(N\) song song với \(A'M\) với cạnh \(BC.\)

Ta có \(C'M = \frac{2}{3}B'C' = 2A,{S_{\Delta A'C'M}} = \frac{1}{2}A'C'.C'M.\sin {60^0} = \frac{1}{2}.3a.2a.\frac{{\sqrt 3 }}{2} = \frac{{3\sqrt 3 {a^2}}}{2}.\)

Lại có \(\frac{{PC}}{{PC'}} = \frac{{CN}}{{A'C'}} = \frac{{CN}}{{AC}} = \frac{1}{4} \Rightarrow \frac{{PC}}{{CC'}} = \frac{1}{3} \Rightarrow PC = \frac{1}{3}.3a = a \Rightarrow PC' = 4a.\)

Thể tích khối chóp \(P.C'A'M\) là \({V_{P.C'A'M}} = \frac{1}{3}.4a.\frac{{3\sqrt 3 {a^2}}}{2} = 2\sqrt 3 {a^3}.\)

Gọi \(E\) là điểm trên cạnh \(BC\) sao cho \(EC = 2EB\) thì \(A'M//AE\) nên

\(\frac{{CQ}}{{CE}} = \frac{{CN}}{{CA}} = \frac{1}{4} \Rightarrow CQ = \frac{1}{4}CE = \frac{1}{4}C'M = \frac{1}{2}a.\)

Ta có \({S_{\Delta CNQ}} = \frac{1}{2}D\left( {N,CQ} \right).CQ = \frac{1}{2}.\frac{1}{4}.d\left( {A,BC} \right).CQ = \frac{1}{8}.\frac{{3a\sqrt 3 }}{2}.\frac{1}{2}a = \frac{{3{a^2}\sqrt 3 }}{{32}}.\)

Thể tích khối chóp \(P.CNQ\) là \({V_{P.CNQ}} = \frac{1}{3}PC.{S_{\Delta CNQ}} = \frac{1}{3}.a.\frac{{3{a^2}\sqrt 3 }}{{32}} = \frac{{{a^3}\sqrt 3 }}{{32}}.\)

Vậy \({V_{CNQ.C'A'M}} = {V_{P.C'A'M}} - {V_{P.CNQ}} = 2\sqrt 3 {a^3} - \frac{{{a^3}\sqrt 3 }}{{32}} = \frac{{63\sqrt 3 {a^3}}}{{32}}.\)

Cách 3:

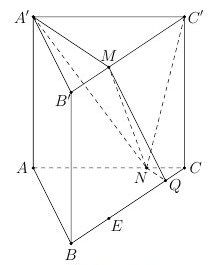
Mặt phẳng \(\left( {A'MN} \right)\) cắt các mặt phẳng \(\left( {ABC} \right)\) và \(\left( {A'B'C'} \right)\) theo các giao tuyến song song nên \(Q\) là giao điểm của đường thẳng qua \(N\) song song với \(A'M\) với cạnh \(BC.\)

Ta có \({V_{CNQ.C'A'M}} = {V_{N.MC'A'}} + {V_{N.CQMC'}}.\)

Ta có \(C'M = \frac{2}{3}B'C' = 2A,{S_{\Delta A'C'M}} = \frac{1}{2}A'C'.C'M.\sin {60^0} = \frac{1}{2}.3a.2a.\frac{{\sqrt 3 }}{2} = \frac{{3\sqrt 3 {a^2}}}{2}.\)

\({V_{CNQ.C'A'M}} = \frac{1}{3}.CC'.{S_{A'C'M}} = \frac{1}{3}.3a.\frac{{3\sqrt 3 {a^2}}}{2} = \frac{{3\sqrt 3 {a^3}}}{2}.\)

Gọi \(E\) là điểm trên cạnh \(BC\) sao cho \(EC = 2EB\) thì \(A'M//AE\) nên \(NQ//AE,\) ta có:

\(\frac{{CQ}}{{CE}} = \frac{{CN}}{{CA}} = \frac{1}{4} \Rightarrow CQ = \frac{1}{4}CE = \frac{1}{4}C'M = \frac{1}{2}a.\)

Diện tích hình thang \(CQMC'\) là \({S_{\Delta CQNC'}} = \frac{1}{2}CC'\left( {CQ + C'M} \right) = \frac{1}{2}.3a.\left( {\frac{1}{2}a + 2a} \right) = \frac{{15{a^2}}}{4}.\)

Thể tích khối chóp \(N.CQMC'\) là

\({V_{N.CQMC'}} = \frac{1}{3}.d\left( {N,\left( {CQMC'} \right)} \right).{S_{CQNC'}} = \frac{1}{3}.\frac{1}{4}d\left( {A,\left( {BCC'B'} \right)} \right).{S_{CQNC'}} = \frac{1}{{12}}.\frac{{3a\sqrt 3 }}{2}.\frac{{15{a^2}}}{4} = \frac{{15\sqrt 3 {a^3}}}{{32}}.\)

Thể tích khối đa diện cần tìm là

\({V_{CNQ.C'A'M}} = {V_{N.MC'A'}} + {V_{N.CQMC'}} = \frac{{3\sqrt 3 {a^3}}}{2} + \frac{{15\sqrt 3 {a^3}}}{{32}} = \frac{{63\sqrt 3 {a^3}}}{{32}}.\)

Đáp án B