Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=căn(6-x) + căn(x-4)+ căn((6-x)&(x-4)) là M,m
Câu hỏi :
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \sqrt {6 - x} + \sqrt {x - 4} + \sqrt {\left( {6 - x} \right)\left( {x - 4} \right)} \) là \(M,m.\) Tính tổng \(M + m.\)
A.\(3 + 2\sqrt 2 \).
B.\(2 + \sqrt 2 \).
C.\(2 + 2\sqrt 2 \).
D.\(3 + \sqrt 2 \).
* Đáp án
D
* Hướng dẫn giải
TXĐ: \(D = 4 \le x \le 6.\)
Đặt \(t = \sqrt {6 - x} + \sqrt {x - 4} \Rightarrow \frac{{{t^2}}}{2} - 1 = \sqrt {\left( {6 - x} \right)\left( {x - 4} \right)} .\)
Xét hàm số \(f\left( x \right) = \sqrt {6 - x} + \sqrt {x - 4} \) với \(4 \le x \le 6.\)
Ta có: \(f'\left( x \right) = 0 \Leftrightarrow \sqrt {6 - x} - \sqrt {x - 4} = 0 \Leftrightarrow x = 5.\)
Bảng biến thiên
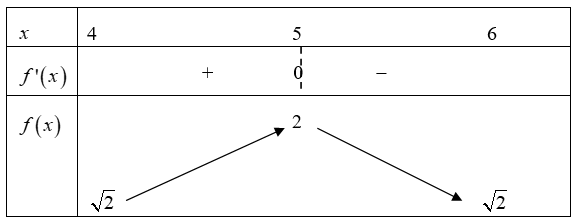
Vậy \(f\left( x \right) \in \left[ {\sqrt 2 ;2} \right] \Rightarrow t \in \left[ {\sqrt 2 ;2} \right]\)
Hàm số đã cho trở thành \(y = f\left( t \right) = \frac{{{t^2}}}{2} + t - 1\) với \(t \in \left[ {\sqrt 2 ;2} \right].\)Khi đó \(y' = t + 1.\) Suy ra \(y' = 0 \Leftrightarrow t = - 1 \notin \left[ {\sqrt 2 ;2} \right].\)
Ta có: \(f\left( {\sqrt 2 } \right) = \sqrt 2 ;f\left( 2 \right) = 3.\) Suy ra \(M = 3,m = \sqrt 2 .\)
Vậy \(M + m = 3 + \sqrt 2 .\)
Đáp án D
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề) !!
Copyright © 2021 HOCTAP247
