Cho mặt nón tròn xoay đỉnh S đáy là đường tròn tâm O có thiết diện qua trục là một tam giác đều cạnh bằng a

* Hướng dẫn giải

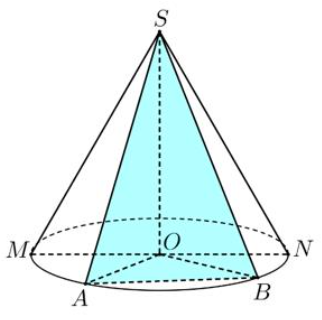
Gọi \(\widehat {AOB} = \alpha .\) Hình chóp \(S.OAB \Rightarrow {0^0} < \alpha < {180^0} \Rightarrow 0 < \sin \alpha \le 1\)

Diện tích \(\Delta OAB\) là \(\frac{1}{2}.OA.ON.\sin \alpha \Rightarrow \) Thể tích khối chóp \(S.OAB\) là \(V = \frac{1}{6}.SO.OA.OB.\sin \alpha \)

Vì thiết diện qua trục là một tam giác đều cạnh bằng \(a \Rightarrow SO = \frac{{a\sqrt 3 }}{2};OA = OB = \frac{a}{2}\)

\( \Rightarrow V = \frac{1}{6}.\frac{{a\sqrt 3 }}{2}.\frac{a}{2}.\frac{a}{2}.\sin \alpha = \frac{{{a^3}\sqrt 3 .\sin \alpha }}{{48}} \le \frac{{{a^3}\sqrt 3 }}{{48}}\)

Dấu “=” xảy ra \( \Leftrightarrow \sin \alpha = 1 \Leftrightarrow \alpha = {90^0} \Leftrightarrow OA \bot OB\)

Vậy thể thchs khối chóp \(S.OAB\) đạt giá trị lớn nhất bằng \[\frac{{{a^3}\sqrt 3 }}{{48}}.\]

Đáp án D