Cho tứ diện ABCD có độ dài cạnh bằng a, (S) là mặt tiếp xúc với sáu cạnh của tứ diện ABCD. M là một điểm thay đổi

* Hướng dẫn giải

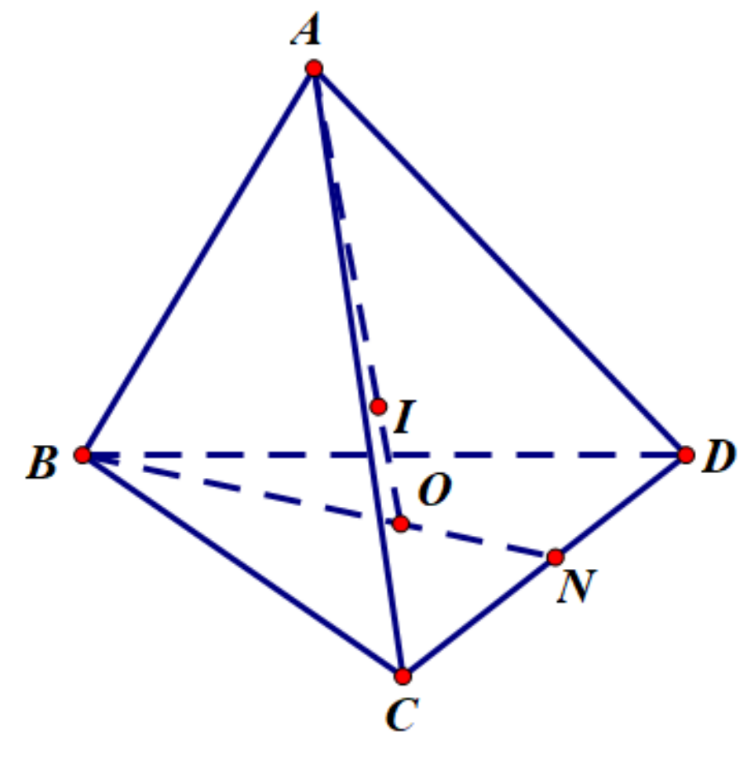
Gọi I là tâm mặt cầu (S) thì I là tâm của tứ diện ABCD.

Gọi N là trung điểm của CD, O là tâm của tam giác BCD.

Ta có:

\[\begin{array}{l}BO = \frac{2}{3}BN = \frac{{a\sqrt 3 }}{3},ON = \frac{1}{3}BN = \frac{{a\sqrt 3 }}{6}\\AO = \sqrt {A{B^2} - B{O^2}} = \frac{{a\sqrt 6 }}{3}\\AI = \frac{3}{4}AO = \frac{{a\sqrt 6 }}{4},OI = \frac{1}{4}AO = \frac{{a\sqrt 6 }}{{12}}\\IN = \sqrt {O{I^2} + O{N^2}} = \frac{{a\sqrt 2 }}{4}\end{array}\]

Bán kính mặt cầu là \[R = IN = \frac{{a\sqrt 2 }}{4}\]

\[\begin{array}{l}T = M{A^2} + M{B^2} + M{C^2} + M{D^2} = {(\overrightarrow {IM} - \overrightarrow {IA} )^2} + {(\overrightarrow {IM} - \overrightarrow {IB} )^2} + {(\overrightarrow {IM} - \overrightarrow {IC} )^2} + {(\overrightarrow {IM} - \overrightarrow {ID} )^2}\\ = 4{\overrightarrow {IM} ^2} - 2\overrightarrow {IM} (\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} ) + ({\overrightarrow {IA} ^2} + {\overrightarrow {IB} ^2} + {\overrightarrow {IC} ^2} + {\overrightarrow {ID} ^2})\\ = 4{R^2} + 4I{A^2}\\ = 2{a^2}\end{array}\]

Vậy \[T = 2{a^2}\]

Đáp án B