Cho khối chóp S.ABC, đáy ABC là tam giác có AB = AC = a, góc BAC = 60^0, góc SBA = góc SCA = 90^0},

* Hướng dẫn giải

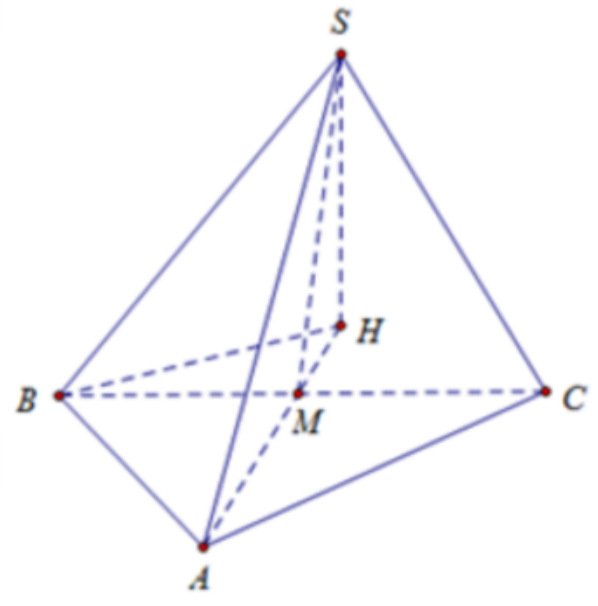
Ta có: \[\Delta SBA = \Delta SCA = >SB = SC\]

Gọi M là trung điểm của BC, ta có:

\[\left\{ \begin{array}{l}SM \bot BC\\AM \bot BC\end{array} \right. = >BC \bot (SAM)\]

Dựng \[SH \bot AM = >SH \bot (ABC)\]. Khi đó \[\widehat {SBH} = {60^o}\]

Do \[S{H^2} + H{B^2} = S{B^2};S{B^2} + A{B^2} = S{A^2}\]

Ta có: \[S{A^2} = S{H^2} + H{B^2} + A{B^2}\], mặt khác \[S{A^2} = H{A^2} + S{H^2}\]

Do đó \[H{B^2} + A{B^2} = H{A^2} = >HB \bot AB\]

Ta có: \[AB = a = >BH = AB\tan \widehat {BAH} = a\sqrt 3 \]

Khi đó:

\[\begin{array}{l}SH = HB\tan {60^o} = 3a;{S_{ABC}} = \frac{{AB.AC.\sin A}}{2} = \frac{{{a^2}\sqrt 3 }}{4}\\ = >V = \frac{1}{3}.SH.{S_{ABC}} = \frac{{{a^3}\sqrt 3 }}{4}\end{array}\]

Đáp án D