Cho phương trình: Gọi S là tập hợp tất cả các giá trị của m nguyên để phương trình đã cho có 6 nghiệm hoặc 7 nghiệm hoặc
Câu hỏi :
Cho phương trình:
A.20.
B.19.
C.14.
D.28.
* Đáp án
D
* Hướng dẫn giải
Ta có:
\({2^{ - \left| {\left| {{m^3}} \right| - 3{m^2} + 1} \right|}}.{\log _{81}}\left( {\left| {\left| {{x^3}} \right| - 3{x^2} + 1} \right| + 2} \right) + {2^{ - \left| {\left| {{x^3}} \right| - 3{x^2} + 1} \right| - 2}}.{\log _3}\left( {\frac{1}{{\left| {\left| {{m^3}} \right| - 3{m^2} + 1} \right| + 2}}} \right) = 0{\rm{ }}\left( 1 \right)\)
\( \Leftrightarrow {2^{ - \left| {\left| {{m^3}} \right| - 3{m^2} + 1} \right| - 2}}.{\log _3}\left( {\left| {\left| {{x^3}} \right| - 3{x^2} + 1} \right| + 2} \right) + {2^{ - \left| {\left| {{x^3}} \right| - 3{x^2} + 1} \right| - 2}}.{\log _3}\left( {\left| {\left| {{m^3}} \right| - 3{m^2} + 1} \right| + 2} \right) = 0\)
\( \Leftrightarrow {2^{\left| {\left| {{x^3}} \right| - 3{m^2} + 1} \right| + 2}}.{\log _3}\left( {\left| {\left| {{x^3}} \right| - 3{x^2} + 1} \right| + 2} \right) = {2^{ - \left| {\left| {{m^3}} \right| - 3{m^2} + 1} \right| + 2}}.{\log _3}\left( {\left| {\left| {{m^3}} \right| - 3{m^2} + 1} \right| + 2} \right){\rm{ }}\left( 2 \right)\)
Xét hàm số \(f\left( t \right) = {2^t}{\log _3}t\) với \(t \ge 2.\)
Có \(f'\left( t \right) = {2^t}\ln 2.{\log _3}t + \frac{{{2^t}}}{{t.\ln 3}} = {2^t}\left( {\ln 2.{{\log }_3}t + \frac{1}{{t.\ln 3}}} \right) >0,\forall c \in \left[ {2; + \infty } \right).\)
Hàm số \(f\left( t \right) = {2^t}{\log _3}t\) đồng biến trên \(\left( {2; + \infty } \right).\)
\(\left( 2 \right) \Leftrightarrow f\left( {\left| {\left| {{x^3}} \right| - 3{x^2} + 1} \right| + 2} \right) = f\left( {\left| {\left| {{m^3}} \right| - 3{m^2} + 1} \right| + 2} \right)\)
\( \Leftrightarrow \left| {\left| {{x^3}} \right| - 3{x^2} + 1} \right| + 2 = \left| {\left| {{m^3}} \right| - 3{m^2} + 1} \right| + 2 \Leftrightarrow \left| {\left| {{x^3}} \right| - 3{x^2} + 1} \right| = \left| {\left| {{m^3}} \right| - 3{m^2} + 1} \right|\)
\( \Leftrightarrow \left[ \begin{array}{l}\left| {{x^3}} \right| - 3{x^2} + 1 = \left| {{m^3}} \right| - 3{m^2} + 1\\\left| {{x^3}} \right| - 3{x^2} + 1 = - \left| {{m^3}} \right| + 3{m^2} - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left| {{x^3}} \right| - 3{x^2} = \left| {{m^3}} \right| - 3{m^2}{\rm{ }}\left( 3 \right)\\\left| {{x^3}} \right| - 3{x^2} = - \left| {{m^3}} \right| + 3{m^2} - 2{\rm{ }}\left( 4 \right)\end{array} \right.\)
Xét hàm số \(g\left( x \right) = {x^3} - 3{x^2}\) có \(g'\left( x \right) = 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right..\)
Ta có bảng biến thiên của hàm số \(g\left( x \right) = {x^3} - 3{x^2}\)
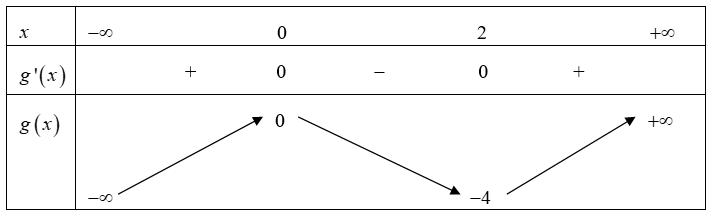
Suy ra bảng biến thiên của hàm số \(g\left( {\left| x \right|} \right) = {\left| x \right|^3} - 3{x^2}\)
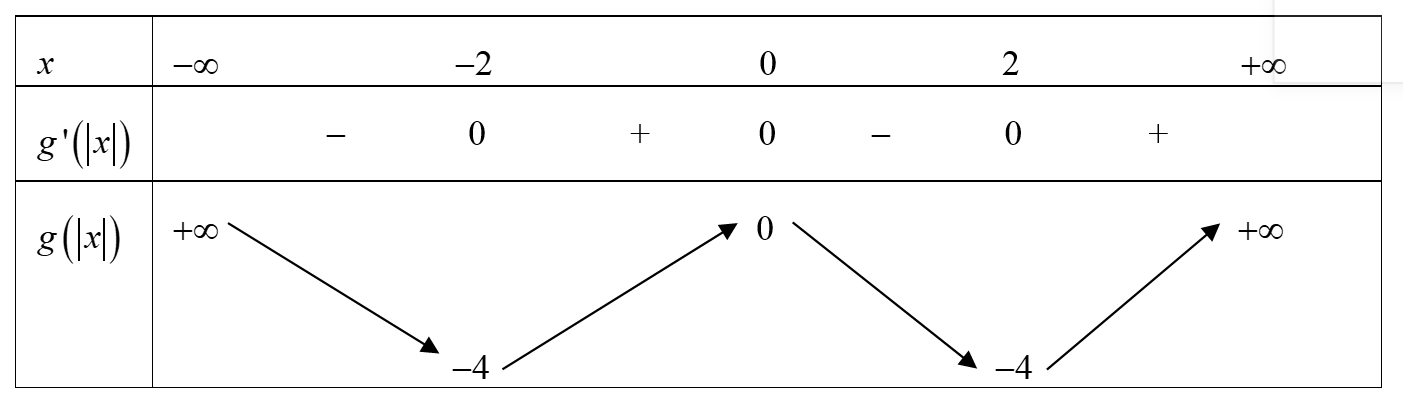
Để phương trình (1) có 6 nghiệm hoặc 7 nghiệm hoặc 8 nghiệm thì phương trình (3) có 4 nghiệm và phương trình (4) có ít nhất 2 nghiệm hoặc phương trình (3) có 3 nghiệm thì phương trình (4) có ít nhất 3 nghiệm hoặc phương trình (3) có 2 nghiệm thì phương trình (4) có 4 nghiệm.
TH1: phương trình (3) có 4 nghiệm và phương trình (4) có ít nhất 2 nghiệm \(\left\{ \begin{array}{l} - 4 < \left| {{m^3}} \right| - 3{m^2} < 0\\ - \left| {{m^3}} \right| + 3{m^2} - 2 \ge - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 4 < \left| {{m^3}} \right| - 3{m^2} < 0\\\left| {{m^3}} \right| - 3{m^2} \le 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left| {{m^3}} \right| - 3{m^2} < 0\\\left| {{m^3}} \right| - 3{m^2} + 4 >0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2}\left( {\left| m \right| - 3} \right) < 0\\{\left( {\left| m \right| - 2} \right)^2}\left( {\left| m \right| + 1} \right) >0\end{array} \right. \Leftrightarrow - 3 < m < 3\)
TH2: phương trình (3) có 3 nghiệm thì phương trình (4) có ít nhất 3 nghiệm \(\left\{ \begin{array}{l}\left| {{m^3}} \right| - 3{m^2} = 0\\ - 4 < - \left| {{m^3}} \right| + 3{m^2} - 2 \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2}\left( {\left| m \right| - 3} \right) = 0\\\left| {{m^3}} \right| - 3{m^2} \ge - 2\\\left| {{m^3}} \right| - 3{m^2} < 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = \pm 3\end{array} \right.\)
TH3: phương trình (3) có 2 nghiệm thì phương trình (4) có 4 nghiệm
\(\left\{ \begin{array}{l}\left[ \begin{array}{l}\left| {{m^3}} \right| - 3{m^2} = - 4\\\left| {{m^3}} \right| - 3{m^2} >0\end{array} \right.\\ - 4 < - \left| {{m^3}} \right| + 3{m^2} - 2 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2}\left( {\left| m \right| - 3} \right) >0\\\left| {{m^3}} \right| - 3{m^2} < 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left| m \right| >3\\\left| {{m^3}} \right| - 3{m^2} < 2\end{array} \right. \Leftrightarrow m \in \emptyset \)
Xét phương trình: \( - \left| {{m^3}} \right| + 3{m^2} - 2 = \left| {{m^3}} \right| - 3{m^2} \Leftrightarrow \left| {{m^3}} \right| - 3{m^2} + 1 = 0\) không có nghiệm nguyên.
Vậy \(S = \left\{ {0; \pm 1; \pm 2; \pm 3} \right\}.\) Tổng bình phương các phần tử của \(S\) là: 28.
Đáp án D
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề) !!
Copyright © 2021 HOCTAP247
