Cho hình nón có bán đáy bằng 2 căn bậc hai của 2. Một mặt phẳng đi qua đỉnh

* Hướng dẫn giải

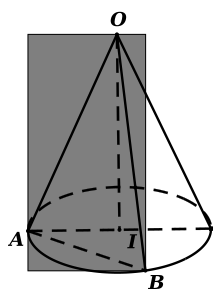
Gọi

\(O\) là đỉnh hình nón, \(I\) là tâm đường tròn đáy hình nón, thiết diện là tam giác đều\(OAB\).

\({S_{OAB}} = \frac{{\sqrt 3 }}{4}O{A^2} = 12\sqrt 3 \Rightarrow O{A^2} = 48\)

Do đó \(OI = \sqrt {O{A^2} - A{I^2}} = \sqrt {48 - 8} = 2\sqrt {10} \)

Thể tích khối nón là: \(V = \frac{1}{3}h.{S_d} = \frac{1}{3}.2\sqrt {10} .\pi .{\left( {2\sqrt 2 } \right)^2} = \frac{{16\sqrt {10} \pi }}{3}\).

Chọn đáp án B