Cho hình chóp S.ABCD có đáy là hình chữ nhật, biết AB = 2a , AD = a, SA = 3a và
Câu hỏi :
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, biết \[AB = 2a,\,\,AD = a,\,\,SA = 3a\] và \(SA\) vuông góc với mặt phẳng đáy. Gọi \(M\) là trung điểm cạnh \(CD\), điểm \(E \in SA\)sao cho \(SE = a\), cosin của góc giữa hai mặt phẳng\(\left( {SAC} \right)\) và \(\left( {BME} \right)\) bằng
A. \(\frac{3}{{2\sqrt {15} }}\).
B. \(\frac{1}{{\sqrt {15} }}\).
C. \(\frac{{\sqrt {14} }}{{\sqrt {15} }}\).
D. \(\frac{{\sqrt {14} }}{{3\sqrt {15} }}\).
* Đáp án
* Hướng dẫn giải
Góc giữa hai mặt phẳng
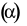 và
và 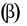 là góc
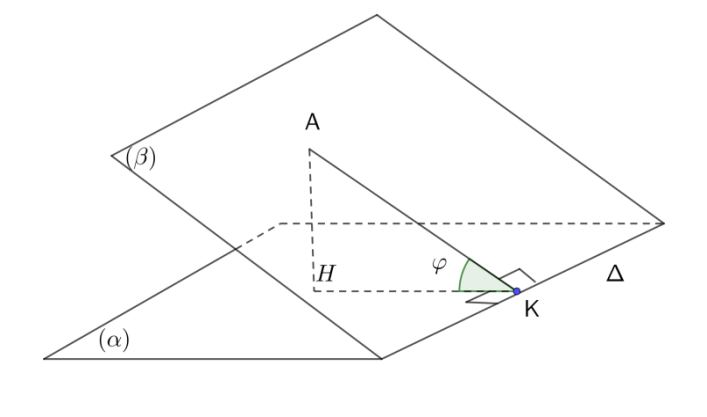
là góc 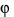 . Khi đó \(\sin \varphi = \frac{{d\left( {A,\alpha } \right)}}{{d\left( {A,\Delta } \right)}}\)
. Khi đó \(\sin \varphi = \frac{{d\left( {A,\alpha } \right)}}{{d\left( {A,\Delta } \right)}}\)
Gọi điểm 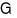 là trọng tâm
là trọng tâm 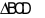 , kéo dài tia
, kéo dài tia 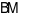 cắt
cắt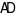 tại
tại 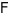 .
. 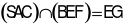 .
.
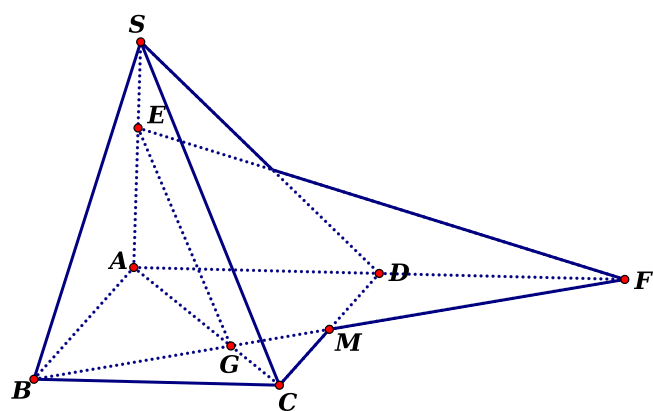
Khi đó góc giữa hai mặt phẳng\(\left( {SAC} \right)\) và \(\left( {BME} \right)\)là góc 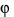 có\(\sin \varphi = \frac{{d\left( {A,\left( {{\rm{BEF}}} \right)} \right)}}{{d\left( {A,EG} \right)}}\) .
có\(\sin \varphi = \frac{{d\left( {A,\left( {{\rm{BEF}}} \right)} \right)}}{{d\left( {A,EG} \right)}}\) .
Ta có \(d\left( {A,\left( {{\rm{BEF}}} \right)} \right) = \frac{{2a\sqrt 3 }}{3}\),\(d\left( {A,EG} \right) = \frac{{AE.AG}}{{\sqrt {A{E^2} + A{G^2}} }} = \frac{{a\sqrt {70} }}{7}\)
\(\sin \varphi = \frac{{d\left( {A,\left( {{\rm{BEF}}} \right)} \right)}}{{d\left( {A,EG} \right)}} = \frac{{\sqrt {14} }}{{\sqrt {15} }} \to {\rm{cos}}\varphi {\rm{ = }}\frac{1}{{\sqrt {15} }}\).
Nhận xét:Bản chất câu 49 khó khăn nhất là việc xác định góc giữa hai mặt phẳng. Tứ diện \(S.ABC\)là một tứ diện đặc biệt được tách từ hình chóp \(S.ABCD\)có \(SD \bot \left( {ABCD} \right)\), mặt đáy là hình vuông. Đây là bài toán khá quen thuộc. Với những bài toán xác định góc phức tạp hơn các em học sinh có thể dùng phương pháp tọa độ.
Chọn đáp án B
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (35 đề) !!
Copyright © 2021 HOCTAP247
