Cho hàm số f(x) có f'(x)=(x-1)^2. (x-2).(x+3). Hàm số f(x) đạt cục tiểu tại điểm nào?

* Hướng dẫn giải

Chọn đáp án C

+) Ta có \(f'(x) = 0\)\( \Leftrightarrow {\left( {x - 1} \right)^2}\left( {x - 2} \right)\left( {x + 3} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = 1\\x = 2\end{array} \right..\)

+) BXD \(f'(x)\):

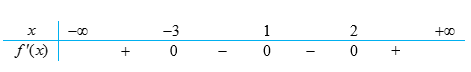
+) Dựa vào bảng xét dấu, ta thấy \(f'(x)\) đổi dấu từ \(\left( - \right)\)sang \(\left( + \right)\)tại \(x = 2\)do đó hàm số \(f\left( x \right)\)đạt cực tiểu tại \(x = 2.\)