Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh a. Góc giữa

* Hướng dẫn giải

Chọn đáp án D

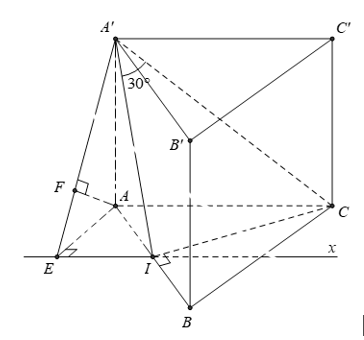
Ta có:

\[\left\{ \begin{array}{l}CI \bot AB\\CI \bot AA'\,\,\,\,\left( {AA' \bot (ABC)} \right)\\{\rm{ }}AB \cap AA' = \{ A\} \\AB,\,AA' \subset \left( {AA'B'A} \right)\quad \end{array} \right.\]\( \Rightarrow CI \bot \left( {AA'B'B} \right)\).

Dễ thấy \[\left( {\widehat {CA';\left( {AA'B'B} \right)}} \right) = \left( {\widehat {CA';IA'}} \right) = \widehat {CA'I} = 30^\circ \].

Do đó \(A'I = \frac{{IC}}{{\tan \widehat {CA'}I}} = \frac{{3a}}{2};\) với \(IC = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\).

Suy ra\(AA' = \sqrt {A'{I^2} - A{I^2}} = \sqrt {\frac{{9{a^2}}}{4} - \frac{{{a^2}}}{4}} = a\sqrt 2 \).

Kẻ \(Ix\parallel AC\). Khi đó \(d(AC,A'I) = d(AC,(A'I,Ix)) = d(A,(A'I,Ix))\)

Kẻ \(AE \bot Ix\) tại \[E\] và \(AF \bot A'E\) tại \[F\].

\[\left\{ \begin{array}{l}EI \bot AE\\EI \bot AA'\,\,\left( {AA' \bot \left( {AEI} \right)} \right)\\AE,\,AA' \subset \left( {A'AE} \right)\\AE \cap AA' = \left\{ A \right\}\end{array} \right. \Rightarrow EI \bot \left( {A'AE} \right) \Rightarrow EI \bot AF\]

Vì\[\left\{ \begin{array}{l}AF \bot A'E\\AF \bot EI\\A'E,EI \subset \left( {A'EI} \right)\\A'E \cap EI = \left\{ E \right\}\end{array} \right. \Rightarrow AF \bot \left( {A'EI} \right)\].

Do đó \(d\left( {A,(A'I,Ix)} \right) = AF\).

Ta có: \(AE = AI.\sin \widehat {AIE} = \frac{a}{2}.\sin 60^\circ = \frac{{a\sqrt 3 }}{4}\) và \(\frac{1}{{A{F^2}}} = \frac{1}{{A'{A^2}}} + \frac{1}{{A{E^2}}} = \frac{1}{{2{a^2}}} + \frac{{16}}{{3{a^2}}} = \frac{{35}}{{6{a^2}}} \Rightarrow AF = \frac{{a\sqrt {210} }}{{35}}\)

Vậy: \(d\left( {AC,A'I} \right) = AF = \frac{{a\sqrt {210} }}{{35}}\).