Cho hình trụ có chiều cao 8a. Biết rằng khi cắt hình trụ đã cho bởi một mặt

* Hướng dẫn giải

Chọn đáp án C

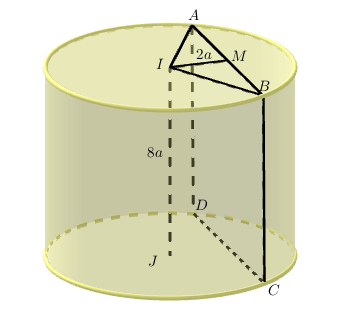
Thiết diện thu được là hình chữ nhật \[ABCD\] với \[AD = BC = IJ = 8a\].

Suy ra \[AB = \frac{{{S_{ABCD}}}}{{BC}} = \frac{{48{a^2}}}{{8a}} = 6a\].

Gọi \[M\] là trung điểm của \[AB\] thì \[AM = \frac{1}{2}AB = 3a\].

Tam giác \[IAB\] cân tại I nên \[IM \bot AB\, \Rightarrow IM\, \bot \,\left( {ABCD} \right)\]. Khi đó \[IM\]là khoảng cách từ trục đến thiết diện.

\[I{A^2} = I{M^2} + A{M^2} = 4{a^2} + 9{a^2} = 13{a^2}\].

Thể tích khối trụ đã cho bằng \[V = \pi .13{a^2}.8a = 104\pi {a^3}\].