Cho hàm số y=f(x)=ax^3 +bx^2+cx+d có đồ thị như hình vẽ:Có bao nhiêu giá trị

* Hướng dẫn giải

Chọn đáp án D

Từ đồ thị, ta thấy

\(f\left( {{{\rm{e}}^x} - x + m} \right) = 1\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{{\rm{e}}^x} - x + m = a}\\{{{\rm{e}}^x} - x + m = 1}\\{{{\rm{e}}^x} - x + m = b}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{{\rm{e}}^x} - x - a = - m}\\{{{\rm{e}}^x} - x - 1 = - m}\\{{{\rm{e}}^x} - x - b = - m}\end{array}} \right.\)

trong đó \(a \in \left( { - 1;0} \right),\) \(b \in \left( {2;3} \right).\)

Xét hàm số \(f\left( x \right) = {{\rm{e}}^x} - x - \alpha \), với \(\alpha \in \left\{ {a;1;b} \right\}\) và \(x \in \mathbb{R}\).

Ta có \(f'\left( x \right) = {{\rm{e}}^x} - 1\) và \(f'\left( x \right) = 0\; \Leftrightarrow x = 0\).

Bảng biến thiên của \(f\left( x \right):\)

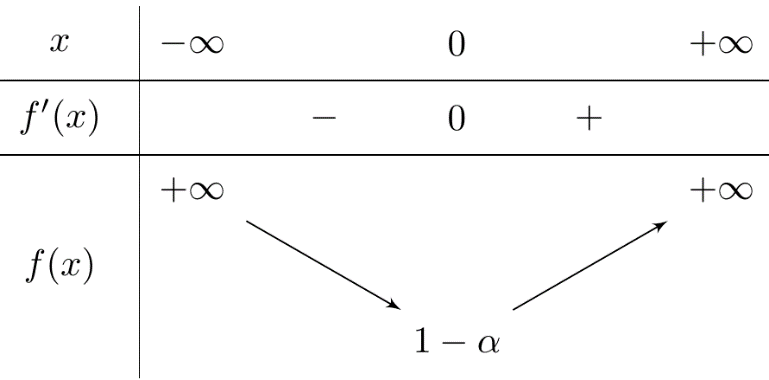
Vì \(a < 0 < 1 < 2 < b\) nên \(1 - a >1 >1 - b\). Do đó, kết hợp với bảng biến thiên ở trên ta thấy rằng, phương trình đã cho có 6 nghiệm phân biệt khi và chỉ khi</>

\( - m >1 - a\; \Leftrightarrow m < a - 1.\)

Vì \( - 1 < a < 0\,\, \Leftrightarrow \,\, - 2 < a - 1 < - 1\) nên các giá trị nguyên của \(m\) trên đoạn \(\left[ { - 10;10} \right]\) là

\( - 10;\; - 9;\; - 8;\; - 7;\; - 6; - 5; - 4; - 3; - 2.\)

Vậy có 9 giá trị nguyên của m thỏa mãn bài toán.