Trang chủ
Đề thi & kiểm tra
Toán học
35 đề minh họa THPT Quốc gia môn Toán năm 2022 có lời giải !!
Cho khối chóp S.ABCD có đáy ABCD là hình chữ...
Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a,SA vuông góc với mặt phẳng đáy và SA=a. Góc giữa hai mặt phẳng SBC và SCD bằng φ, với cosφ=13. Thể tích khối chóp đã cho bằn...
Câu hỏi :
A.
A.
B.
C.
D.
* Đáp án
* Hướng dẫn giải
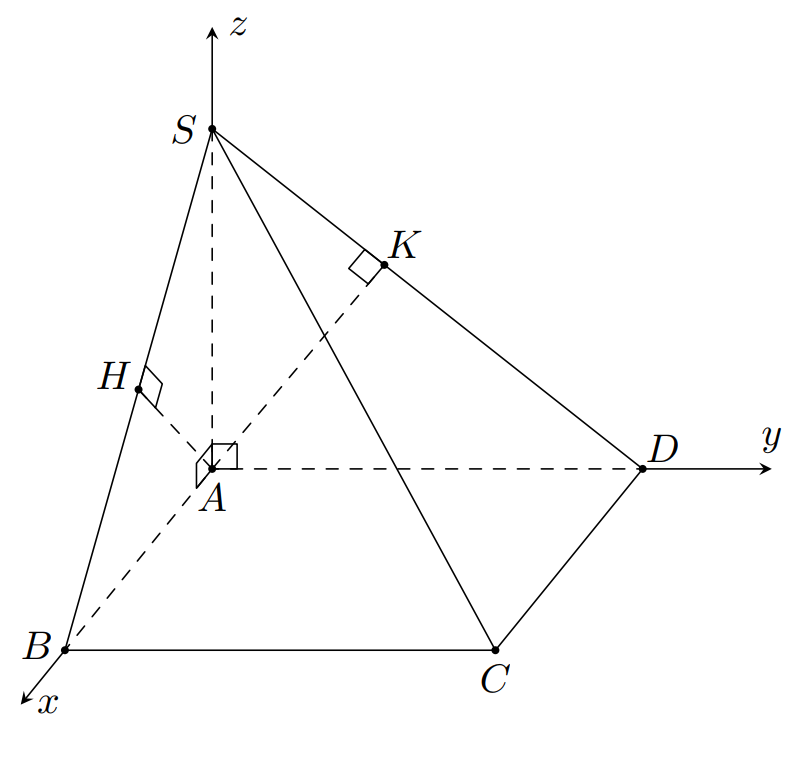
Đặt với
Trong mặt phẳng kẻ tại trong mặt phẳng , kẻ tại
Dễ dàng chứng minh được , và là trung điểm của
Chọn hệ trục tọa độ như hình vẽ
Ta có:
Suy ra:
Trong tam giác vuông tại có
.
Do lần lượt là hai véc-tơ pháp tuyến của hai mặt phẳng và nên
Thể tích khối chóp là
Chọn đáp án B.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
35 đề minh họa THPT Quốc gia môn Toán năm 2022 có lời giải !!
Số câu hỏi: 498
Copyright © 2021 HOCTAP247
