Trong không gian, cho hình thang vuông tại A và D biết AB=a; AD=CD=2a . Khi quay hình thang

* Hướng dẫn giải

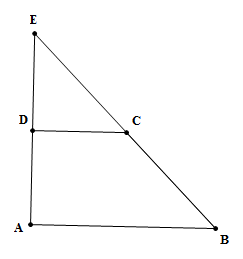
Gọi \(E = AD \cap BC\), dễ thấy \(D\) là trung điểm của \(AE\). Ta có \(AD = DE = CD = a\).

Khi đó thể tích của khối tròn xoay cần tính bằng \({V_1} - {V_2}\). Trong đó:

+) \({V_1}\) là thể tích của khối tròn xoay khi quay đường gấp khúc \(ABE\) quanh trục \(AE\), và \({V_1} = \frac{1}{3}.\pi .{\left( {2a} \right)^2}.2a = \frac{{8\pi {a^3}}}{3}\).

+) \({V_2}\) là thể tích của khối tròn xoay khi quay đường gấp khúc \(DCE\) quanh trục \(DE\) và

\({V_2} = \frac{1}{3}\pi .{a^2}.a = \frac{{\pi {a^3}}}{3}\).

Vậy thể tích của khối tròn xoay cần tính bằng \(\frac{{8\pi {a^3}}}{3} - \frac{{\pi {a^3}}}{3} = \frac{{7\pi {a^3}}}{3}\).

Chọn đáp án B