Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A;B. Gọi G là trọng tâm tam giác

* Hướng dẫn giải

Ta có \[AC = a\sqrt 2 \]. Gọi \[I\] là trung điểm của \[AD\]\[ \Rightarrow CD = \sqrt {C{I^2} + I{D^2}} = a\sqrt 2 \Rightarrow A{D^2} = C{D^2} + A{C^2} \Rightarrow CD \bot AC\]

Mà \[CD \bot SA \Rightarrow CD \bot \left( {SAC} \right)\]

Kẻ \[AH \bot SC \Rightarrow AH \bot \left( {SCD} \right)\] vì \[CD \bot \left( {SAC} \right) \supset AH \Rightarrow AH \bot CD\;\]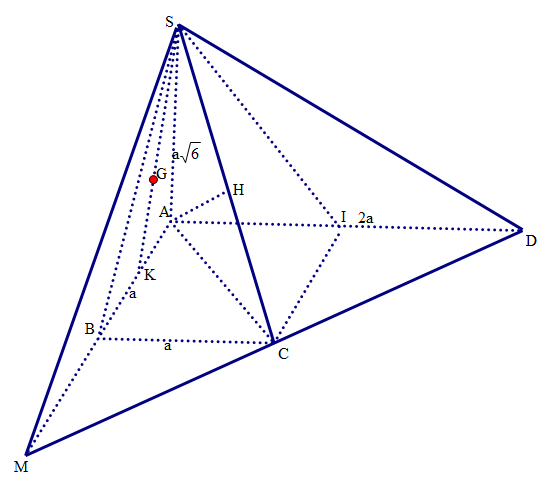

Gọi \[K\] là trung điểm \[AB\], gọi \[M\] là giao điểm của \[CD\] và \[AB\]

Ta có \[d\left( {G,\left( {SCD} \right)} \right) = \frac{2}{3}d\left( {K,\left( {SCD} \right)} \right) = \frac{2}{3}.\frac{3}{4}d\left( {A,\left( {SCD} \right)} \right) = \frac{1}{2}AH\]

Ta có \[AH = \frac{{SA.AC}}{{SC}} = \frac{{a\sqrt 6 .a\sqrt 2 }}{{\sqrt {S{A^2} + A{C^2}} }} = \frac{{a\sqrt 6 .a\sqrt 2 }}{{\sqrt {6{a^2} + 2{a^2}} }} = \frac{{a\sqrt 6 }}{2}\]

Vậy \[d\left( {G,\left( {SCD} \right)} \right) = \frac{{a\sqrt 6 }}{4}\]

Chọn đáp án A