Cho hình nón có chiều cao h=20 cm đường tròn đáy có tâm O bán kính đường tròn đáy

* Hướng dẫn giải

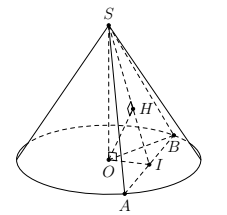Giả sử thiết diện của hình chóp là tam giác \[SAB\], với \[S\] là đỉnh của hình chóp, gọi \[I\] là trung điểm của \[AB\], Gọi \[H\]là hình chiếu vuông góc của \[O\] lên mặt phẳng \[(SAB)\], \[OH\]chính là bán kính mặt cầu tâm \[O\] và tiếp xúc với mặt phẳng thiết diện\[(SAB)\]

Ta có \[AB = 40(cm) \Rightarrow IB = 20(cm)\]

Áp dụng định lí pitago cho tam giác \[OIB\]vuông tại \[I\]

\[OI = \sqrt {O{B^2} - I{B^2}} = \sqrt {{{25}^2} - {{20}^2}} = 15(cm)\]

Xét tam giác \[SOI\] vuông tại \[O\] ta có

\[\frac{1}{{O{H^2}}} = \frac{1}{{{\rm{O}}{{\rm{S}}^2}}} + \frac{1}{{O{I^2}}}\]

\[\frac{1}{{O{H^2}}} = \frac{1}{{{\rm{2}}{{\rm{0}}^2}}} + \frac{1}{{{{15}^2}}} \Rightarrow O{H^2} = 144 \Rightarrow OH = 12(cm)\]

\[S = 4\pi {r^2} = 4.\pi {.12^2} = 576\pi (c{m^2})\]

Chọn đáp án A