Cho tứ diện đều ABCDcó cạnh bằng a. Gọi M,N lần lượt là trung điểm của các cạnh

* Hướng dẫn giải

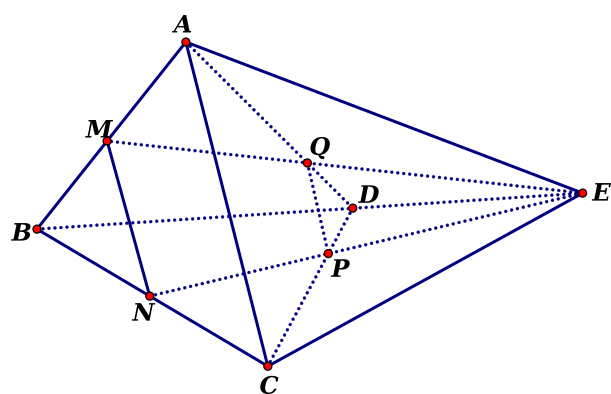
Gọi \(P = EN \cap CD\)và \(Q = EM \cap AD\).

Suy ra \[P,{\rm{ }}Q\] lần lượt là trọng tâm của \[\Delta BCE\]và \[\Delta ABE\].

Gọi \[S\] là diện tích tam giác \[BCD\], suy ra \({S_{\Delta CDE}} = {S_{\Delta BNE}} = S.\)

Ta có \[{S_{\Delta PDE}} = \frac{1}{3}.{S_{\Delta CDE}} = \frac{S}{3}.\]

Gọi \[h\] là chiều cao của tứ diện \[ABCD\], suy ra

\[d\left[ {M,\left( {BCD} \right)} \right] = \frac{h}{2};{\rm{ }}\,d\left[ {Q,\left( {BCD} \right)} \right] = \frac{h}{3}.\]

Khi đó \[{V_{M.BNE}} = \frac{1}{3}{S_{\Delta BNE}}.d\left[ {M,\left( {BCD} \right)} \right] = \frac{{S.h}}{6};\]\[{V_{Q.PDE}} = \frac{1}{3}{S_{\Delta PDE}}.d\left[ {Q,\left( {BCD} \right)} \right] = \frac{{S.h}}{{27}}.\]

Suy ra \[{V_{PQD.NMB}} = {V_{M.BNE}} - {V_{Q.PDE}} = \frac{{S.h}}{6} - \frac{{S.h}}{{27}} = \frac{{7S.h}}{{54}} = \frac{7}{{18}}.\frac{{S.h}}{3} = \frac{7}{{18}}.{V_{ABCD}}\]

\[ \Rightarrow V' = V - \frac{7}{{18}}.{V_{}} = \frac{{11}}{{18}}V \Rightarrow \frac{{V'}}{V} = \frac{{11}}{{18}}\].

Vậy \(\frac{{V'}}{V} = \frac{{11}}{{18}}\).

Chọn đáp án B