Cho hình nón có thiết diện qua trục là tam giác vuông cân có cạnh huyền bằng

* Hướng dẫn giải

Chọn đáp án B

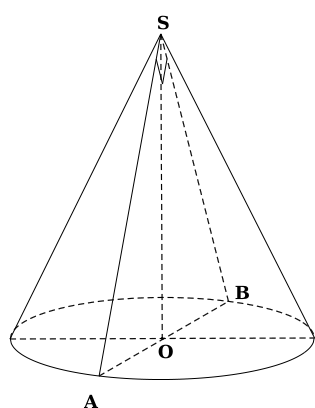
Thiết diện qua trục là tam giác \(\Delta SAB\) vuông cân tại \(S\), có \(AB = 2a\sqrt 2 \) nên

bán kính đáy \(r = \frac{{AB}}{2} = a\sqrt 2 \)

Đường sinh \(l = SA = \sqrt {\frac{{A{B^2}}}{2}} = \sqrt {\frac{{{{\left( {2a\sqrt 2 } \right)}^2}}}{2}} = 2a\)

Vậy diện tích xung quanh của hình nón là \({S_{xq}} = \pi rl = \pi .a\sqrt 2 .2a = 2\sqrt 2 \pi {a^2}\).