Khi cắt khối trụ (T) bởi một mặt phẳng song song với trục và cách trục

* Hướng dẫn giải

Chọn đáp án D

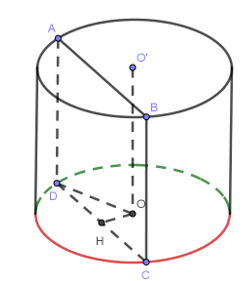
Thiết diện là hình vuông \(ABCD\). Gọi \(H\) là trung điểm đoạn \(CD\).

Ta có: \(\left\{ \begin{array}{l}OH \bot CD\\OH \bot AD\end{array} \right. \Rightarrow OH \bot \left( {ABCD} \right)\).

Do đó: \(d\left( {O'O,\left( {ABCD} \right)} \right) = d\left( {O,\left( {ABCD} \right)} \right) = OH = a\sqrt 2 \).

Ta có: \({S_{ABCD}} = D{C^2} = 8{a^2} \Rightarrow h = AD = DC = \sqrt {8{a^2}} = 2\sqrt 2 a \Rightarrow DH = a\sqrt 2 \).

Ta có: \(R = OD = \sqrt {O{H^2} + D{H^2}} = 2a\).

Vậy \({S_{tp}} = 2\pi Rh + 2\pi {R^2} = 2\pi .2a.2\sqrt 2 a + 2\pi .4{a^2} = \left( {8 + 8\sqrt 2 } \right)\pi {a^2}\).