Cho hình chóp S.ABCD có chiều cao bằng 12 và diện tích đáy bằng 27.

* Hướng dẫn giải

Chọn đáp án D

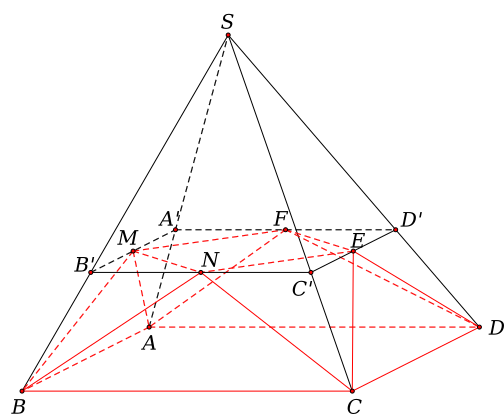
Chiều cao khối chóp \(S.ABCD\) là \(h = 12\) và diện tích đáy là \(S = 27\). Gọi \(A'\), \(B'\), \(C'\), \(D'\) lần lượt là các điểm nằm trên các cạnh \(SA\), \(SB\), \(SC\), \(SD\) sao cho \(\frac{{SA'}}{{SA}} = \frac{{SB'}}{{SB}} = \frac{{SC'}}{{SC}} = \frac{{SD'}}{{SD}} = \frac{2}{3}\).

Diện tích hình bình hành \(A'B'C'D'\) là \(S' = \frac{2}{3}.\frac{2}{3}.S = \frac{4}{9}.S\).

Diện tích tam giác \(B'MN\) bằng \(\frac{1}{8}S' = \frac{1}{8}.\frac{4}{9}S = \frac{1}{{18}}S\).

Thể tích khối chóp \(B.B'MN\) là \({V_1} = \frac{1}{3}.\frac{1}{{18}}S.\frac{1}{3}h = \frac{1}{{162}}.Sh\).

Thể tích khối chóp cụt \(A'B'C'D'.ABCD\) là \(V' = \frac{1}{3}S.h - \frac{1}{3}.\frac{4}{9}S.\frac{2}{3}h = \frac{{19}}{{81}}Sh\).

Thể tích khối đa diện lồi cần tìm là \(V = V' - 4{V_1} = \frac{{19}}{{81}}Sh - 4.\frac{1}{{162}}Sh = \frac{{17}}{{81}}Sh = \frac{{17}}{{81}}.27.12 = 68\).