Cho hình chóp S.ABCD có SB vuông góc (ABC) và SB = 4,AC = 2, góc (ABC) bằng 60 độ
Câu hỏi :
Cho hình chóp \(S.ABC\) có \(SB \bot (ABC)\) và SB=4 ,AC = 2, góc ABC=60 độ. Tính diện tích mặt cầu ngoại tiếp hình chóp \(SABC\).
A. \(\frac{{48\pi }}{3}\).
B. \(\frac{{80\pi }}{3}\).
C. \(\frac{{64\pi }}{3}\).
D. \(\frac{{32\pi }}{3}\).
* Đáp án
* Hướng dẫn giải
Lời giải
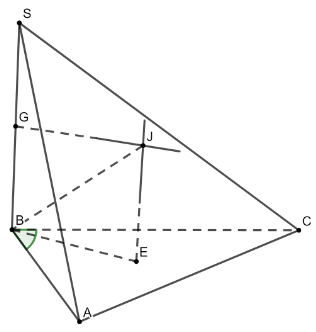
* Gọi \(G\) là trung điểm của \(SB,\) \(E\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). Dựng đường thẳng \(d\) qua \(E\) và vuông góc với mặt phẳng \(\left( {ABC} \right)\). Khi đó, đường thẳng \(d\)song song với \(SB\). Trong mặt phẳng \(\left( {SB,d} \right)\) đường trung trực của cạnh \(SB\)qua trung điểm \(G\)và cắt đường thẳng \(d\) tại \(J\) \( \Rightarrow \) \(J\) là tâm mặt cầu ngoại tiếp hình chóp \(SABC\) và bán kính mặt cầu là \(R = JB\).
* Xét tam giác \(ABC\) với \(R = EB\) là bán kính đường tròn ngoại tiếp, ta có:
\({S_{ABC}} = \frac{1}{2}BA.BC.\sin \widehat {ABC} = \frac{{BA.BC.AC}}{{4R}}\)\( \Rightarrow R = EB = \frac{{2AC}}{{4\sin \widehat {ABC}}} = \frac{2}{{\sqrt 3 }}\)
Xét tam giác vuông \(BEJ\), vuông tại \(E\), ta có: \(EB = \frac{2}{{\sqrt 3 }}\), \(EJ = BG = \frac{1}{2}SB = 2\)
\( \Rightarrow R = JB = \sqrt {E{B^2} + E{J^2}} = \frac{{4\sqrt 3 }}{3}\).
Vậy diện tích mặt cầu là \({S_C} = 4\pi .{R^2} = 4\pi .\frac{{16}}{3} = \frac{{64\pi }}{3}\).
Chọn đáp án C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (35 đề) !!
Copyright © 2021 HOCTAP247
