Trong không gian biết tập hợp các điểm (M left( {x ,; ,y ,; ,z} right) ) thỏa mãn ( left| x right| + left| y right| = 1 ,, , left| z right| le 1 ), làm thành các mặt bên của một kh...

* Hướng dẫn giải

Lời giải

Ta có:

\(\begin{array}{l}\left| x \right| + \left| y \right| = 1 \Leftrightarrow \left| y \right| = 1 - \left| x \right| \Leftrightarrow \left[ \begin{array}{l}y = 1 - \left| x \right|\\y = \left| x \right| - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}y = - x + 1\\y = x + 1\\y = - x - 1\\y = x - 1\end{array} \right.\\\end{array}\)

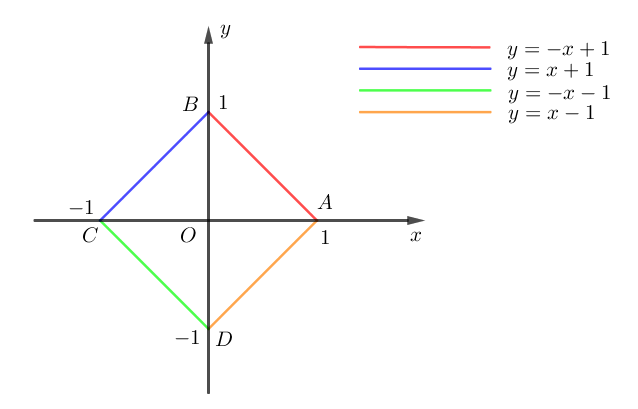
Với \(\left| z \right| \le 1 \Leftrightarrow - 1 \le z \le 1\).

Vậy tập hợp các điểm \(M\left( {x\,;\,y\,;\,z} \right)\) là khối lăng trụ có đáy là hình vuông \(ABCD\), chiều cao \(h = 2\).

\(OA = 1 \Rightarrow AB = \sqrt 2 \Rightarrow {S_{ABCD}} = 2\).

\( \Rightarrow V = h\,.\,{S_{ABC{\rm{D}}}}\, = 2.\,2 = 4\).

Chọn đáp án D