Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và AC=a Biết tam giác

* Hướng dẫn giải

Lời giải

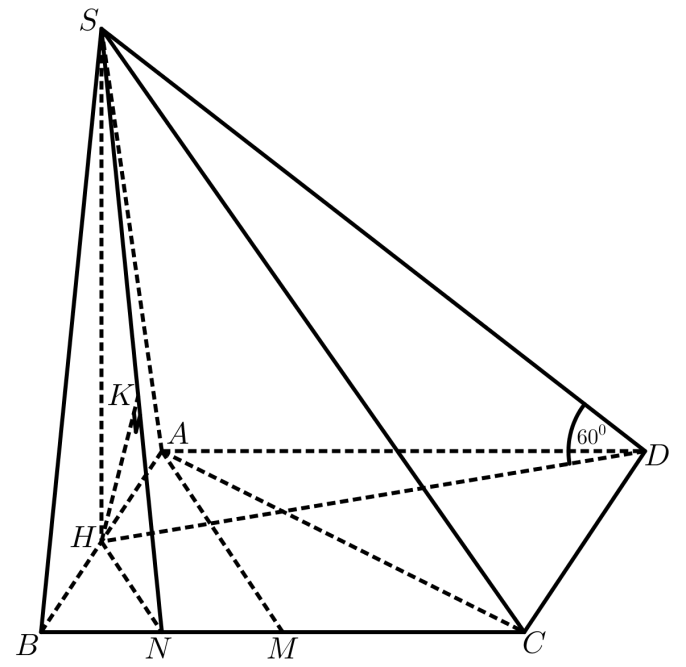
Gọi \(H\) là trung điểm \(AB.\) Theo giả thiết ta có \(SH \bot \left( {ABCD} \right).\)

Vì \(AC = a\) nên tam giác \(ABC\) đều.

Theo giả thiết \(\left( {SD,\,\,\left( {ABCD} \right)} \right) = \widehat {SDH} = 60^\circ .\)

Ta có \(AD{\rm{//}}BC \Rightarrow AD{\rm{//}}\left( {SBC} \right).\)

Khi đó \(d\left( {AD,\,\,SC} \right) = d\left( {AD,\,\,\left( {SBC} \right)} \right) = d\left( {A,\,\,\left( {SBC} \right)} \right) = 2d\left( {H,\,\,\left( {SBC} \right)} \right).\)

Gọi \(M\) là trung điểm \(BC \Rightarrow AM \bot BC.\)

Vẽ \(HN \bot BC\) (1) \(\left( {N \in BC} \right),\) \(HK \bot SN\) (2) \(\left( {K \in SN} \right).\)

\(SH \bot \left( {ABCD} \right) \Rightarrow SH \bot BC\) (3).

(1), (3) \( \Rightarrow BC \bot \left( {SHN} \right) \Rightarrow BC \bot HK\) (4).

(2), (4) \( \Rightarrow HK \bot \left( {SBC} \right).\)

Khi đó \(d\left( {H,\,\,\left( {SBC} \right)} \right) = HK.\)

\(HN = \frac{1}{2}AM = \frac{{a\sqrt 3 }}{4}.\)

\(H{D^2} = A{H^2} + A{D^2} - 2.AH.AD.\cos \widehat {HAD} = \frac{{7{a^2}}}{4} \Rightarrow HD = \frac{{a\sqrt 7 }}{2}.\)

\(\tan \widehat {SDH} = \frac{{SH}}{{HD}} \Leftrightarrow SH = HD.\tan \widehat {SDH} = \frac{{a\sqrt {21} }}{2}.\)

\(\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{N^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt {21} }}{2}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{4}} \right)}^2}}} = \frac{{116}}{{21{a^2}}} \Rightarrow HK = \frac{{\sqrt {609} }}{{58}}a.\)

Vậy \(d\left( {AD,\,\,SC} \right) = 2.\frac{{\sqrt {609} }}{{58}}a = \frac{{\sqrt {609} a}}{{29}}.\)

Chọn đáp án B