Cho f(x) là hàm số đa thức có một phần đồ thị của hàm f'(x) như hình vẽ bên.
Câu hỏi :
Cho \[f\left( x \right)\] là hàm số đa thức có một phần đồ thị của hàm \[f'\left( x \right)\] như hình vẽ bên. Gọi \[F\left( x \right)\] là một nguyên hàm của hàm số \[f\left( x \right)\]. Tìm tất cả các giá trị của tham số \[m\] để hàm số \[y = F\left( x \right) + \left( {m - 1} \right)x + 2020\] đồng biến trên khoảng \[\left( { - 1\,;\,4} \right)\].
A. \[m >1 - f\left( { - 1} \right)\].
B. \[m \ge 1 - f\left( { - 1} \right)\].
C. \[m \ge 1 - f\left( 4 \right)\].
D. \[m >1 - f\left( 4 \right)\].
* Đáp án
* Hướng dẫn giải
Lời giải
\[F\left( x \right)\] là một nguyên hàm của \[f\left( x \right) \Rightarrow F'\left( x \right) = f\left( x \right)\].
Hàm số \[y = F\left( x \right) + \left( {m - 1} \right)x + 2020\] đồng biến trên khoảng \[\left( { - 1\,;\,4} \right)\] khi
\[y' = F'\left( x \right) + m - 1 \ge 0\,\,\forall x \in \left( { - 1\,;\,4} \right) \Rightarrow f\left( x \right) + m - 1 \ge 0\,\,\forall x \in \left( { - 1\,;\,4} \right) \Rightarrow 1 - m \le f\left( x \right)\,\,\forall x \in \left( { - 1\,;\,4} \right)\].
Gọi \[{S_1},\,{S_2}\] lần lượt là diện tích hình phẳng giới hạn bởi đồ thị của \[f'\left( x \right)\] với trục hoành trên các đoạn \[\left[ { - 1\,;\,1} \right]\] và \[\left[ {1\,;\,4} \right]\]. Từ đồ thị \[ \Rightarrow {S_1} < {S_2}\].
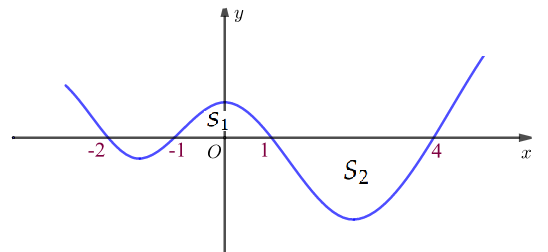
Ta có \[f\left( 4 \right) - f\left( { - 1} \right) = \int\limits_{ - 1}^4 {f'\left( x \right){\rm{d}}x = \int\limits_{ - 1}^1 {f'\left( x \right){\rm{d}}x + \int\limits_1^4 {f'\left( x \right){\rm{d}}x} } } = {S_1} - {S_2} < 0 \Rightarrow f\left( 4 \right) < f\left( { - 1} \right)\].
Từ đó ta có bảng biến thiên sau:
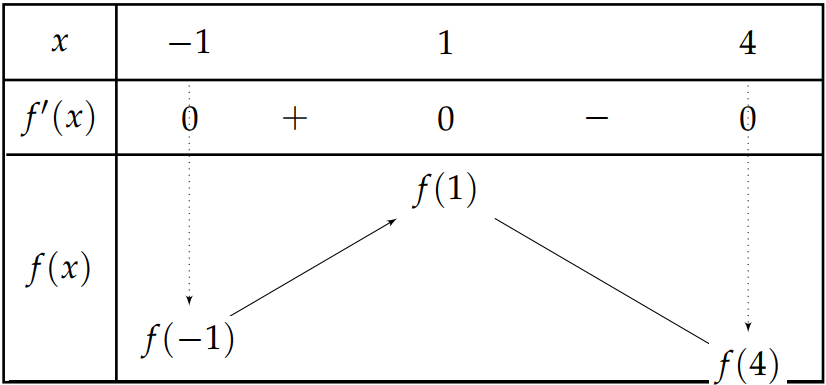
Do \[f\left( x \right)\] là hàm đa thức nên liên tục trên \[\left[ { - 1\,;\,4} \right]\], do đó từ bảng biến thiên, ta có \[1 - m \le f\left( x \right)\,\forall x \in \left( { - 1\,;\,4} \right) \Leftrightarrow 1 - m \le f\left( 4 \right) \Rightarrow m \ge 1 - f\left( 4 \right)\].
Chọn đáp án C
</></>
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (35 đề) !!
Copyright © 2021 HOCTAP247
