Cho khối lăng trụ ABC.A'B'C' đáy là tam giác vuông cân tại A. Hình chiếu của A' lên

* Hướng dẫn giải

Lời giải

Gọi K là trung điểm \[A'B'\] ta có:

+) \[B'KHB\] là hình bình hành nên \[HB'\] cắt \[BK\] tại trung điểm \[I\] của mỗi đường.

\[\begin{array}{l} + )\,BK\parallel A'H \Leftarrow A'H\parallel (BKC') \Rightarrow d(A'H,BC') = d(A'H,(BKC')) = d(H,(BKC'))\\ = d(B',(BKC')) = d = \frac{{4\sqrt 5 }}{5}.\end{array}\]

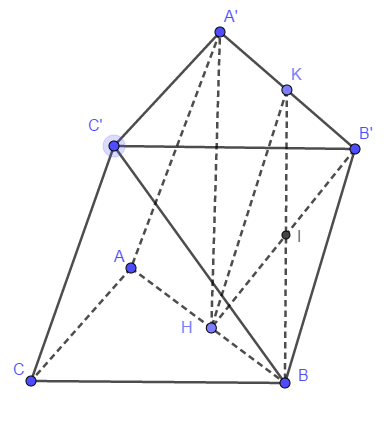
Đặt \[AB = 2x \Rightarrow A'C' = 2x\,.\] (Do đáy là tam giác vuông cân tại \[A\]).

Ta có

\[\begin{array}{l}KC' = \sqrt {A'C{'^2} + A'{K^2}} = x\sqrt {5.} \\KB = A'H = \sqrt {AA{'^2} - A{H^2}} = \sqrt {9 - {x^2}} .\end{array}\]

Xét tứ diện \[B'BC'K\] với đáy là \[\Delta BC'K\] vuông tại \[K\] có \[{S_{BC'K}} = \frac{1}{2}.KC'.BK. = \frac{1}{2}.x\sqrt 5 .\sqrt {9 - {x^2}} .\] và độ dài đường cao là \[d\].\[ \Rightarrow {V_{B'.BCK}} = \frac{1}{3}d.{S_{BKC'}} = \frac{1}{3}.\frac{{4\sqrt 5 }}{5}.\frac{1}{2}x\sqrt 5 .\sqrt {9 - {x^2}} \,\, = \frac{2}{3}\,x.\sqrt {9 - {x^2}} .\,\] (1)

Mặt khác, \[{V_{B'.BCK}} = \frac{1}{6}{V_{ABC.A'B'C'}} = \frac{1}{6}.A'H.{S_{ABC}} = \frac{1}{6}.\sqrt {9 - {x^2}} \,.\frac{1}{2}2x.2x = \frac{1}{3}\,{x^2}.\sqrt {9 - {x^2}} .\,\,(2)\]

Từ (1) và (2) suy ra \[\frac{2}{3}\,x.\sqrt {9 - {x^2}} = \frac{1}{3}\,{x^2}.\sqrt {9 - {x^2}} \Leftrightarrow x = 2.\] \[A'H = \sqrt 5 .\]

Vậy thể tích khối lăng trụ

\[{V_{ABC.A'B'C'}} = A'H.{S_{ABC}} = \sqrt 5 .\frac{1}{2}.{(2x)^2} = \sqrt 5 .\frac{1}{2}.{(2.2)^2} = 8\sqrt 5 .\]

Chọn đáp án B