Cho hàm số y= trị tuyệt đối của (1/(x+3) - 1/x + 1/(x+2) -1/(x-5) -m)

* Hướng dẫn giải

Lời giải

Yêu cầu bài toán \( \Leftrightarrow \) Phương trình \(\frac{1}{{x + 3}} - \frac{1}{x} + \frac{1}{{x - 2}} - \frac{1}{{x - 5}} - m = 0\) vô nghiệm trên \(\left( { - 3\,;5} \right)\backslash \left\{ {0\,;2} \right\}\).

Ta có \(\frac{1}{{x + 3}} - \frac{1}{x} + \frac{1}{{x - 2}} - \frac{1}{{x - 5}} - m = 0 \Leftrightarrow \frac{2}{{{x^2} - 2x}} - \frac{8}{{{x^2} - 2x - 15}} = m\).

Đặt \(t = {x^2} - 2x\). Do \(x \in \left( { - 3\,;5} \right)\backslash \left\{ {0\,;2} \right\} \Rightarrow t \in \left[ { - 1\,;15} \right)\backslash \left\{ 0 \right\}\).

Phương trình trở thành \(\frac{2}{t} - \frac{8}{{t - 15}} = m\).

Xét hàm số \(f\left( t \right) = \frac{2}{t} - \frac{8}{{t - 15}},\,\,t \in \left[ { - 1\,;15} \right)\backslash \left\{ 0 \right\}.\)

Ta có \(f'\left( t \right) = - \frac{2}{{{t^2}}} + \frac{8}{{{{\left( {t - 15} \right)}^2}}}.\)

\(f'\left( t \right) = 0 \Leftrightarrow - \frac{2}{{{t^2}}} + \frac{8}{{{{\left( {t - 15} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}t = 5\\t = - 15\end{array} \right.\)

Bảng biến thiên:

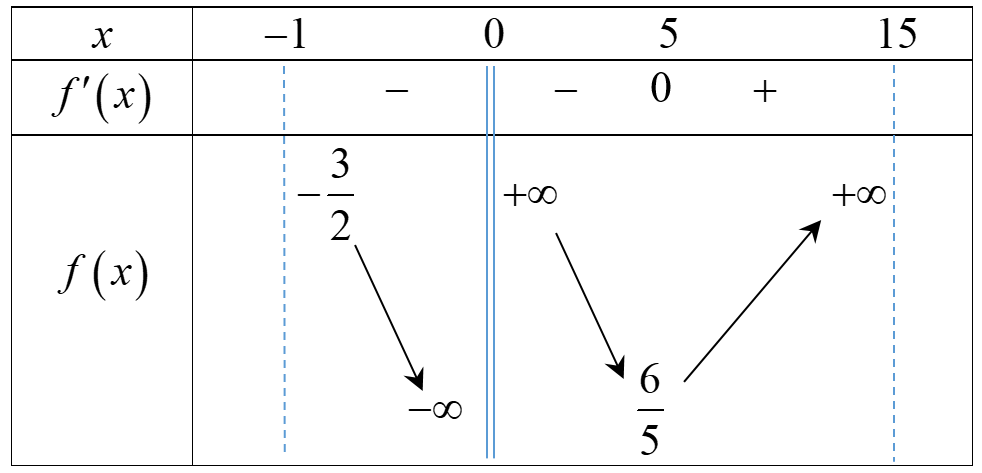
Từ bảng biến thiên suy ra \( - \frac{3}{2} < m < \frac{6}{5}\). Từ đó suy ra \(m \in \left\{ { - 1\,;0\,;1} \right\}\).

Chọn đáp án A