Cho hình hộp chữ nhật ABCD.A'B'C'D'. Gọi N là trung điểm của B'C', (P)

* Hướng dẫn giải

Lời giải

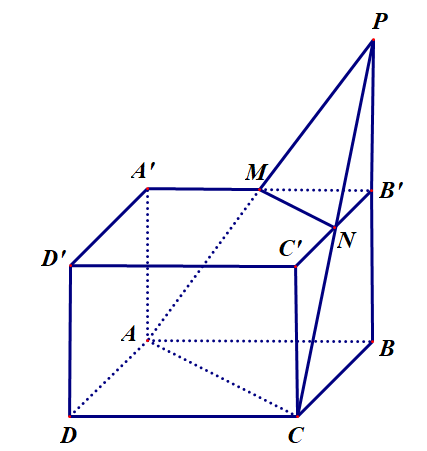
Gọi

\(M\) là trung điểm của \(A'B'\). Mặt phẳng \(\left( {PAC} \right)\) chia khối hộp chữ nhật thành hai phần như hình vẽ. Gọi thể tích khối hộp chữ nhật ban đầu là \(V\), phần chứa điểm \(B'\) có thể tích \({V_1}\) và phần còn lại có thể tích \({V_2}\).

Ta có \(\frac{{PB'}}{{PB}} = \frac{{PN}}{{PC}} = \frac{{PM}}{{PA}} = \frac{{MB'}}{{AB}} = \frac{1}{2}\).

Thể tích của khối chóp \(P.ACB\) là \({V_{P.ACB}} = \frac{1}{3}PB.{S_{ABC}} = \frac{1}{3}.2.BB'.\frac{1}{2}.AB.BC = \frac{1}{3}V\).

Ta lại có \(\frac{{{V_{P.MNB'}}}}{{{V_{P.ACB}}}} = \frac{{PB'}}{{PB}}.\frac{{PN}}{{PC}}.\frac{{PM}}{{PA}} = \frac{1}{8}\).

Do đó \({V_1} = {V_{P.ACB}} - {V_{P.MNB'}} = \left( {1 - \frac{1}{8}} \right){V_{P.ACB}} = \frac{7}{8}.\frac{1}{3}{V_{ABCD.A'B'C'D'}} = \frac{7}{{24}}V\).

Vậy \[\frac{{{V_1}}}{{{V_2}}} = \frac{{{V_1}}}{{V - {V_1}}} = \frac{{7V}}{{24\left( {V - \frac{7}{{24}}V} \right)}} = \frac{7}{{17}}\].