Cho hàm y=f(x) = x^4 -6x^3+ 12x^2 - (2m-1)x + 3m + 2, với m là tham số thực

* Hướng dẫn giải

Chọn đáp án A

Ta có \(f'\left( x \right) = 4{x^3} - 18{x^2} + 24x - \left( {2m - 1} \right)\).

\(YCBT \Leftrightarrow f\left( x \right)\) có đúng 3 điểm cực trị dương \( \Leftrightarrow f'\left( x \right) = 0\) có đúng 3 nghiệm dương phân biệt

\( \Leftrightarrow 2m - 1 = 4{x^3} - 18{x^2} + 24x\) có đúng 3 nghiệm dương phân biệt.

Xét hàm số \(g\left( x \right) = 4{x^3} - 18{x^2} + 24x \Rightarrow g'\left( x \right) = 12{x^2} - 36x + 24 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\)

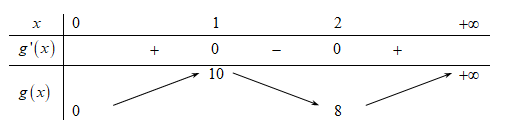
Do đó \(8 < 2m - 1 < 10 \Leftrightarrow \frac{9}{2} < m < \frac{{11}}{2} \Rightarrow m = 5\).