Tìm số nghiệm thực của phương trình (trị tuyệt đối của x-1) ^2 . e^(trị tuyệt đối x-1)

* Hướng dẫn giải

Chọn đáp án B

Đặt \(t = \left| x \right| - 1 \ge - 1\), với mỗi giá trị \(t >- 1\) thì cho ta 2 giá trị của x.

Xét hàm số \(f\left( t \right) = {t^2}{e^t}\), với \(t \ge - 1\) ta có \(\left\{ \begin{array}{l}t >- 1\\f'\left( t \right) = 2t{e^t} + {t^2}{e^t} = 0\end{array} \right. \Leftrightarrow t = 0\).

Xét bảng sau:

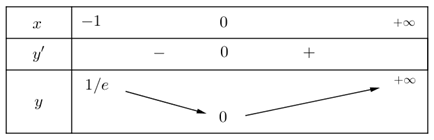
Từ đó phương trình \({t^2}{e^t} = \log 2\) có đúng 2 nghiệm thực phân biệt lớn hơn 1.

Do đó phương trình đã cho có đúng 4 nghiệm thực phân biệt.