Trang chủ
Đề thi & kiểm tra
Toán học
Đề minh họa THPT Quốc gia môn Toán năm 2022 chọn lọc, có lời giải (30 đề) !!
Cho hàm số y=f(x) có đạo hàmf'(x)=(x+1)^4(x-m)^5(x+3)^3 với mọi .
Cho hàm số y=f(x) có đạo hàmf'(x)=(x+1)^4(x-m)^5(x+3)^3 với mọi .
Câu hỏi :
A. 5
A. 5
B. 4
C. 3
D. 6
* Đáp án
* Hướng dẫn giải
Do hàm số có đạo hàm với mọi nên liên tục trên R, do đó hàm số liên tục trên R. Suy ra là một số hữu hạn.
Xét trên khoảng :
- TH1: thì . Khi đó là nghiệm bội lẻ của nên đổi dấu một lần qua suy ra hàm số có duy nhất một điểm cực trị là .
- TH2: thì vô nghiệm, suy ra với mọi
Hàm số đồng biến trên khoảng
Cả hai trường hợp trên đều có: hàm số có duy nhất một điểm cực trị là .
- TH 3: thì là nghiệm bội lẻ của
Bảng biến thiên của hàm số
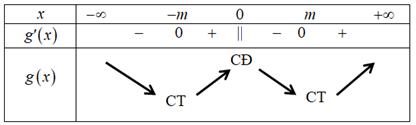
- Lại có và m nguyên nên .
Vậy có 5 giá trị nguyên của m.
Xét trên khoảng :
- TH1: thì . Khi đó là nghiệm bội lẻ của nên đổi dấu một lần qua suy ra hàm số có duy nhất một điểm cực trị là .
- TH2: thì vô nghiệm, suy ra với mọi
Hàm số đồng biến trên khoảng
Cả hai trường hợp trên đều có: hàm số có duy nhất một điểm cực trị là .
- TH 3: thì là nghiệm bội lẻ của
Bảng biến thiên của hàm số
- Lại có và m nguyên nên .
Vậy có 5 giá trị nguyên của m.
Chọn đáp án A
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề minh họa THPT Quốc gia môn Toán năm 2022 chọn lọc, có lời giải (30 đề) !!
Số câu hỏi: 1483
Copyright © 2021 HOCTAP247
