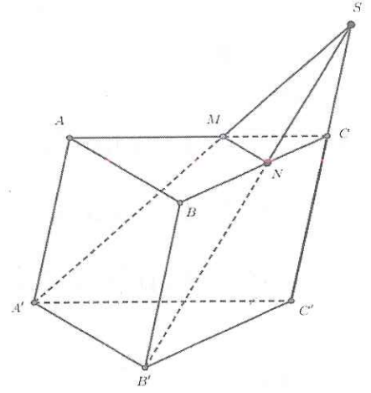
Cho hình lăng trụ ABC.A'B'C' và M, N là hai điểm lần lượt trên cạnh CA, CB sao cho MN song song với AB và CMCA=k. Mặt phẳng MNB'A' chia khối lăng trụ ABC.A'B'C' thành hai phần có t...

Câu hỏi :

Cho hình lăng trụ $ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ và M, N là hai điểm lần lượt trên cạnh CA, CB sao cho MN song song với AB và $\frac{CM}{CA}=k$. Mặt phẳng $\left(MN{B}^{\text{'}}{A}^{\text{'}}\right)$ chia khối lăng trụ $ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ thành hai phần có thể tích $V_1$ (phần chứa điểm C) và $V_2$ sao cho $\frac{V_1}{V_2}=2$. Khi đó giá trị của k là