Cho hàm số f(x) , hàm số y=f'(x) liên tục trên R và có đồ thị như hình vẽ.

* Hướng dẫn giải

Đáp án C

Ta có: $f\left(x\right)>2x+m,\forall x\in \left(-1;2\right)\iff m<f\left(x\right)-2x,\forall x\in \left(-1;2\right)\left(*\right)$.

Dựa vào đồ thị hàm số $y=f\text{'}\left(x\right)$ ta có với $x\in \left(-1;2\right)$ thì $f\text{'}\left(x\right)>2$.

Xét hàm số $g\left(x\right)=f\left(x\right)-2x$ trên khoảng (-1;2).

$g\text{'}\left(x\right)=f\text{'}\left(x\right)-2>\mathrm{0,}\forall x\in \left(-1;2\right)$.

Suy ra hàm số g(x) đồng biến trên khoảng (-1;2).

Do đó $\left(*\right)\iff m\le g\left(-1\right)\iff m\le f\left(-1\right)+2$.

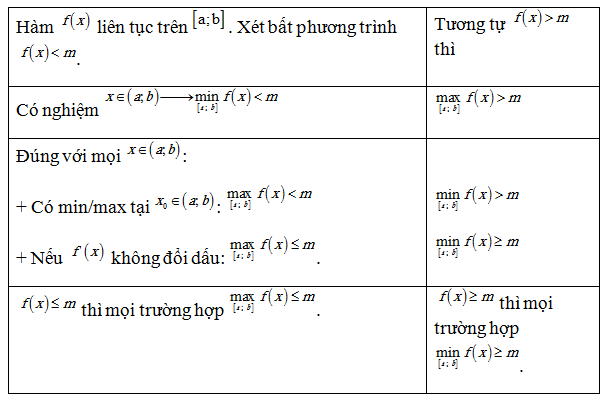
Nhận xét:

Với dạng toán này hướng đi bài toán là cô lập m, khi đó bài toán có thể chuyển sang dạng $m\ge \max g\left(x\right)$ hoặc $m\le \min g\left(x\right)$

Từ đó xét hàm số g(x) và tìm giá trị lớn nhất hoặc giá trị nhỏ nhất (tùy vào bài)