Trang chủ
Đề thi & kiểm tra
Toán học
Đề thi thử THPT QG năm 2021 !!
Trong không gian với hệ tọa độ Oxyz, cho mặt...
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (s)= x^2+y^2+z^2-2x-4y+6z-13=0 và điểm M nằm ngoài mặt cầu
Câu hỏi :
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu và điểm M nằm ngoài mặt cầu sao cho từ M kẻ được ba tiếp tuyến MA, MB, MC đến mặt cầu (A, B, C là các tiếp điểm) và . Khi đó, thể tích khối chóp M.ABC bằng:
A.
B.
C.
D.
* Đáp án
B
* Hướng dẫn giải
Đáp án B
- Mặt cầu có tâm , bán kính .
Ta có: .vuông tại B.
Gọi J là trung điểm .
Do nên tại J.
Tam giác MIC vuông tại .
Xét vuông tại J,
.
Vậy thể tích cần tìm: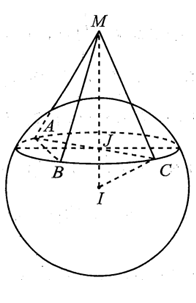
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 !!
Số câu hỏi: 200
Copyright © 2021 HOCTAP247
