Trang chủ
Đề thi & kiểm tra
Toán học
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (35 đề) !!
Trong không gian, cho hình chữ nhật ABCD có AB=6cm...
Trong không gian, cho hình chữ nhật ABCD có AB=6cm và BC=2 cm
Câu hỏi :
Trong không gian, cho hình chữ nhật ABCDcó \[AB = 6{\mkern 1mu} {\rm{cm}}\] và \[BC = 2{\mkern 1mu} {\rm{cm}}.\] Gọi M, N lần lượt là trung điểm của các cạnh BC và CD. Tính thể tích V của khối tròn xoay, nhận được khi quay đa giác \[ABMND\] xung quanh trục AD.
A.\[V = 54\pi {\mkern 1mu} {\rm{c}}{{\rm{m}}^3}.\]
B.\[V = 63\pi {\mkern 1mu} {\rm{c}}{{\rm{m}}^3}.\]
C.\[V = 72\pi {\mkern 1mu} {\rm{c}}{{\rm{m}}^3}.\]
D.\[V = 69\pi {\mkern 1mu} {\rm{c}}{{\rm{m}}^3}.\]
* Đáp án
* Hướng dẫn giải
Lời giải:
Chọn đáp án D
Ta có \(V = {V_{tru}} - {V_{non}} = \pi A{B^2}.AD - \frac{1}{3}\pi C{N^2}.MC.\)
\(AB = 6;AD = 2;CN = \frac{{AB}}{2} = 3;CM = \frac{{BC}}{2} = 1\)\( \Rightarrow V = 69\pi c{m^3}.\)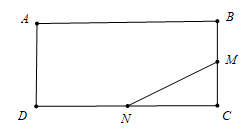
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (35 đề) !!
Số câu hỏi: 399
Copyright © 2021 HOCTAP247
