Phương trình 2020^x + 1/(6-x)-1/(x-12)

* Hướng dẫn giải

Lời giải:

Chọn đáp án A

Điều kiện \(x \ne 6;x \ne 12\).

Xét hàm số \(f\left( x \right) = {2020^x} + \frac{1}{{6 - x}} - \frac{1}{{x - 12}} - 2019\), với \(x \in \left( { - \infty ;1} \right)\) ta có:

\(f'\left( x \right) = {2020^x}\ln 2020 + \frac{1}{{{{\left( {x - 6} \right)}^2}}} + \frac{1}{{{{\left( {x - 12} \right)}^2}}} >0,\forall x \in \left( { - \infty ;6} \right)\)

\( \Rightarrow f\left( x \right)\) đồng biến trên \(\left( { - \infty ;6} \right)\).

Do đó trên \(\left( { - \infty ;6} \right)\) phương trình \(f\left( x \right) = 0\) nếu có nghiệm thì sẽ có nghiệm duy nhất.

Xét bảng sau:

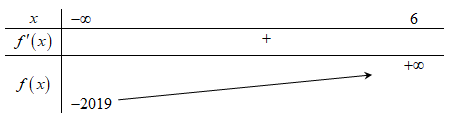
Đường thẳng \(y = 0\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại đúng một điểm nên \(f\left( x \right) = 0\) có nghiệm duy nhất trên \(\left( { - \infty ;6} \right)\).

Do đó phương trình đã cho có nghiệm duy nhất trên \(\left( { - \infty ;6} \right)\).

Tương tự, trên \(\left( {6;12} \right)\) phương trình đã cho có nghiệm duy nhất.

Trên \(\left( {12; + \infty } \right)\) phương trình đã cho có nghiệm duy nhất.

Vậy phương trình đã cho có đúng 3 nghiệm thực