Trang chủ
Đề thi & kiểm tra
Toán học
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (35 đề) !!
Cho hình thang ABCD có góc BAD = góc ADC...
Cho hình thang ABCD có góc BAD = góc ADC = 90 độ
Câu hỏi :
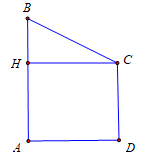
Cho hình thang \[ABCD\] có \[\widehat {BAD} = \widehat {ADC} = 90^\circ \] và \[AB = 8,{\rm{ }}CD = BC = 5.\] Tính thể tích V của khối tròn xoay, nhận được khi quay hình thang \[ABCD\] xung quanh trục \[AB.\]
A.\[V = \frac{{128\pi }}{3}.\]
B.\[V = 128\pi .\]
C.\[V = \frac{{256\pi }}{3}.\]
D.\[V = 96\pi .\]
* Đáp án
* Hướng dẫn giải
Chọn đáp án D
Kẻ \(CH \bot AB\).
Ta có \(V = {V_{non}} + {V_{tru}} = \frac{1}{3}\pi H{C^2}.BH + \pi A{D^2}.AH.\)
\(HC = AD = \sqrt {B{C^2} - B{H^2}} = \sqrt {B{C^2} - {{\left( {AB - CD} \right)}^2}} = 4\)
\( \Rightarrow V = \frac{1}{3}\pi {.4^2}.3 + \pi {.4^2}.5 = 96\pi .\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (35 đề) !!
Số câu hỏi: 399
Copyright © 2021 HOCTAP247
