Trong không gian Oxyz,cho mặt cầu (S1)= (x-1)^2 + (y-1)^2

* Hướng dẫn giải

Chọn đáp án D

Mặt cầu \(\left( {{S_1}} \right)\) có tâm \({I_1}\left( {1;1;2} \right)\) và bán kính \({R_1} = 4\).

Mặt cầu \(\left( {{S_2}} \right)\) có tâm \({I_2}\left( { - 1;2; - 1} \right)\) và bán kính \({R_2} = 3\).

Ta có \(\overrightarrow {{I_1}{I_2}} = \left( { - 2;1; - 3} \right) \Rightarrow {I_1}{I_2} = \sqrt {14} \).

Gọi Ilà tâm của đường tròn giao tuyến \(\left( C \right)\) và Alà một điểm thuộc \(\left( C \right)\).

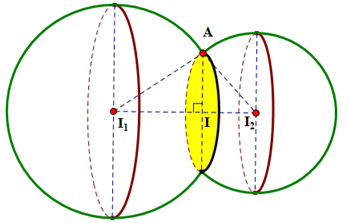
Ta có \(16 - 9 = - 4{\rm{x}} + 2y - 6{\rm{z}} \Leftrightarrow 4{\rm{x}} - 2y + 6{\rm{z}} + 7 = 0\).

Gọi \(\left( P \right)\) là mặt phẳng chứa đường tròn giao tuyến của hai mặt cầu \(\left( {{S_1}} \right)\) và \(\left( {{S_2}} \right)\)

\( \Rightarrow \left( P \right):4{\rm{x}} - 2y + 6{\rm{z}} + 7 = 0 \Rightarrow {I_1}I = d\left( {{I_1};(P)} \right) = \frac{{21}}{{2\sqrt {14} }}\).

\(\overrightarrow {{I_1}I} = \frac{{\left| {\overrightarrow {{I_1}I} } \right|}}{{\left| {\overrightarrow {{I_1}{I_2}} } \right|}}.\overrightarrow {{I_1}{I_2}} = \frac{{\frac{{21}}{{2\sqrt {14} }}}}{{\sqrt {14} }}.\overrightarrow {{I_1}{I_2}} = \frac{3}{4}.\overrightarrow {{I_1}{I_2}} \Leftrightarrow \left\{ \begin{array}{l}{x_I} - 1 = \frac{3}{4}.\left( { - 2} \right)\\{y_I} - 1 = \frac{3}{4}.1\\{z_I} - 2 = \frac{3}{4}.\left( { - 3} \right)\end{array} \right. \Rightarrow I\left( { - \frac{1}{2};\frac{7}{4}; - \frac{1}{4}} \right)\).

\({I_1}I = {I_1}A.\cos \widehat {A{I_1}I} = {R_1}.\cos \widehat {A{I_1}{I_2}}\)

\( = {R_1}.\frac{{{I_1}{A^2} + {I_1}I_2^2 - AI_2^2}}{{2.{I_1}A.{I_1}{I_2}}} = 4.\frac{{{4^2} + 14 - {3^2}}}{{2.4.\sqrt {14} }} = \frac{{21}}{{2\sqrt {14} }}.\)