Cho hình chóp đều S.ABC có góc ASB = 30 độ ; SA =1 . Lấy điểm B’, C’ lần lượt thuộc cạnh SB, SC

* Hướng dẫn giải

Đáp án D

Cắt tứ diện theo các cạnh SA, AC, AB rồi trải lên mặt phẳng (SBC)

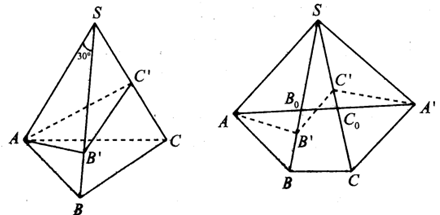
Tam giác SBC giữ nguyên, tam giác SAB lật thành tam giác SAB; tam giác SAC thành tam giác SCA’.

Do đó: $AC\text{'}=A\text{'}C\text{'};SA\text{'}=SA=1$ 

$\widehat{A_{1}S{A}_2}=\widehat{A_{1}SB}+\widehat{BSC}+\widehat{CS{A}_2}=3.30={90}^o$ và $SA\text{'}=SA=1$ nên $\Delta SAA\text{'}$ là tam giác vuông cân.

$C_{AB\text{'}C\text{'}}=AB\text{'}+B\text{'}C\text{'}+AC\text{'}=AB\text{'}+B\text{'}C\text{'}+A\text{'}C\text{'}\ge AA\text{'}=\sqrt{2}$  không đổi,

Dấu “=” xảy ra khi và chỉ khi A, B’, C’, A’ thẳng hàng tức là khi $B\text{'}\equiv B_o,C\text{'}\equiv C_o$ 

Ta có $\frac{SB\text{'}}{SB}=\frac{S{B}_o}{SB}=\frac{S{B}_0}{SA}=\frac{\sin \widehat{SA{B}_o}}{\sin \widehat{S{B}_{o}A}}=\frac{\sin {45}^o}{\sin {105}^o}=-1+\sqrt{3}$ 

Vậy $\frac{V_{S.AB\text{'}C\text{'}}}{V_{S.ABC}}=\frac{SB\text{'}}{SB}.\frac{SC\text{'}}{SC}={\left(\frac{SB\text{'}}{SB}\right)}^2=4-2\sqrt{3}\Rightarrow 3a+4b=4$