Trang chủ
Đề thi & kiểm tra
Toán học
Đề thi thử THPT QG năm 2021 !!
Tất cả các giá trị thực của tham số m...
Tất cả các giá trị thực của tham số m để hai đường cong c1: y=x^3
Câu hỏi :
Tất cả các giá trị thực của tham số m để hai đường cong và có 4 tiếp tuyến chung là
A.
B.
C.
D.
A. Hàm số đồng biến trên khoảng
* Đáp án
C
* Hướng dẫn giải
Đáp án C
Phương trình tiếp tuyến tại điểm của đồ thị hàm số là
Phương trình tiếp tuyến tại điểm của đồ thị hàm số là
Để hai đồ thị hàm số có tiếp tuyến chung thì
Xét
Khi đó
Bảng biến thiên
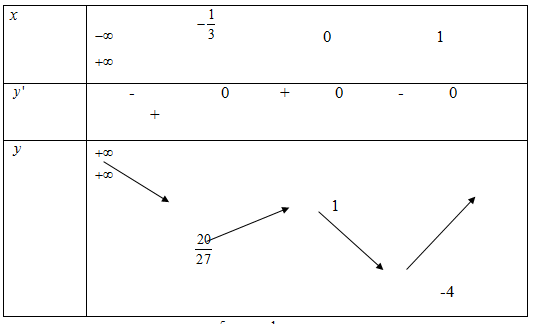
Do đó phương trình có 4 nghiệm khi
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 !!
Số câu hỏi: 200
Copyright © 2021 HOCTAP247
