Cho số phức z=x+yi(x;y thuộc R) thỏa mãn|z ngang +2-3i|<=|z-2+i|<=5 . Gọi m, M lần lượt là giá trị lớn nhất,

Gọi $N\left(x;y\right)$ là điểm biểu diễn cho số phức $z=x+yi$ 

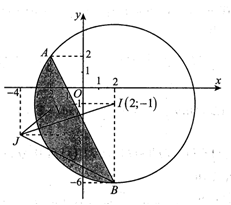
Ta có: $\left|\overline{z}+2-3i\right|\le \left|z-2+i\right|\iff 2x+y+2\le 0;\left|z-2+i\right|\le 5\iff {\left(x-2\right)}^2+{\left(y+1\right)}^2\le 25$  (hình tròn tâm $I\left(2;-1\right)$, bán kính $r=5)$. Tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện $\left|\overline{z}+2-3i\right|\le \left|z-2+i\right|\le 5$  thuộc miền (T) (xem hình vẽ với $A\left(-2;2\right);B\left(2;-6\right)$).

Ta có $P+25={\left(x+4\right)}^2+{\left(y+3\right)}^2\Rightarrow \sqrt{P+25}=\sqrt{{\left(x+4\right)}^2+{\left(y+3\right)}^2}=NJ$ (với $J\left(-4;-3\right))$ 

Bài toán trở thành tìm điểm N thuộc miền (T) sao cho NJ đạt giá trị lớn nhất, nhỏ nhất.

Ta có: $IJ-r\le NJ\le JB\iff 2\sqrt{10}-5\le \sqrt{P+25}\le 3\sqrt{5}\iff 40-20\sqrt{10}\le P\le 20$ 

Vậy $m+M=60-20\sqrt{10}$