Cho hàm số Y=F(X) bảng biến thiên như sau: Số giá trị nguyên của tham số m để phương trình f(x^2-4)=m có ít nhất 3 nghiệm thực phân biệt thuộc khoảng là

Đặt $t=x^2-4x\Rightarrow t\text{'}=2x-4$

Cho $t\text{'}=0\iff x=2$ (nhận)

Bảng biến thiên:

$\Rightarrow t\in [-4;+\infty )$

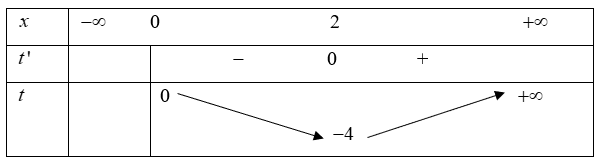
Dựa vào bảng biến thiên ta có

Nếu $[\begin{array}{l}t=-4\\ t\ge 0\end{array}$ khi đó với một giá trị t cho duy nhất một giá trị x thuộc khoảng $(0;+\infty )$

Nếu $t\in (-4;0)$ khi đó với một giá trị t cho hai giá trị x thuộc khoảng $t\in (-4;0)$

Như vậy dựa trên bảng biến thiên của hàm số $y=f\left(x\right),$ phương trình có ít nhất ba nghiệm thuộc khoảng $(0;+\infty )$ khi $m\in (-3;2].$ Vậy có 5 giá trị nguyên m nên chọn đáp án C.