Cho tứ diện đều ABCD M là trung điểm của BC. Khi đó cos của góc giữa hai đường thẳng nào sau đây có giá trị bằng

* Hướng dẫn giải

Phương pháp giải:

Sử dụng định lí Cô-sin trong tam giác.

Giải chi tiết:

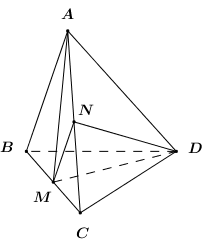
Ta có $\cos \alpha =\frac{\sqrt{3}}{6}\iff \alpha >{60}^0$.

Xét đáp án A: $\angle (AB;AM)=\angle BAM$.

Vì $\Delta ABC$ đều nên AM là phân giác của $\angle BAC\Rightarrow \angle BAM={30}^0$.

Do đó loại đáp án A.

Xét đáp án B và C: Giả sử ABCD là tứ diện đều cạnh 1.

Xét tam giác AMD có $AM=DM=\frac{\sqrt{3}}{2}$.

Áp dụng định lí Cô-sin trong tam giác AMD có:

$\cos \angle AMD=\frac{A{M}^2+M{D}^2-A{D}^2}{2AM.MD}$$=\frac{\frac{3}{4}+\frac{3}{4}-1}{2.\frac{3}{4}}=\frac{1}{3}$

$\Rightarrow \cos (AM;DM)=\frac{1}{3}$⇒ Loại đáp án B.

\[\cos \angle ADM = \frac{{A{D^2} + M{D^2} - A{M^2}}}{{2AD.MD}}\] $=\frac{1+\frac{3}{4}-\frac{3}{4}}{\mathrm{2.1.}\frac{\sqrt{3}}{2}}=\frac{\sqrt{3}}{3}$$\Rightarrow \cos (AD;DM)=\frac{\sqrt{3}}{3}$⇒ Loại đáp án B.

Xét đáp án D: Gọi N là trung điểm của AC.

Ta có $MN//AB\Rightarrow \angle (AB;DM)=\angle (MN;DM)$.

Ta có $MN=\frac{1}{2}AB=\frac{1}{2};DM=\frac{\sqrt{3}}{2};DM=\frac{\sqrt{3}}{2}$.

Áp dụng định lí Cô-sin trong tam giác DMNcó:

$\cos \angle DMN=\frac{D{M}^2+M{N}^2-D{N}^2}{2DM.MN}$

$=\frac{\frac{3}{4}+\frac{1}{4}-\frac{3}{4}}{2.\frac{\sqrt{3}}{2}.\frac{1}{2}}=\frac{\sqrt{3}}{6}$$\Rightarrow \cos (AB;DM)=\frac{\sqrt{3}}{6}$(thỏa mãn).

Đáp án A.