(VD): Hỏi có bao nhiêu giá trị m nguyên trong [-2020;2020] để phương trình log(mx)=2log(x+1) có nghiệm duy nhất?

* Hướng dẫn giải

Phương pháp giải:

- Tìm ĐKXĐ của phương trình.

- Đưa về cùng cơ số 10.

- Giải phương trình logarit: ${\log }_{a}f\left(x\right)={\log }_{a}g\left(x\right)\iff f\left(x\right)=g\left(x\right)>0$.

- Cô lập m, đưa phương trình về dạng $m=f\left(x\right)$.

- Lập BBT của hàm số f(x), từ BBT tìm điều kiện của m để phương trình vô nghiệm.

Giải chi tiết:

ĐKXĐ: \[\left\{ {\begin{array}{*{20}{l}}{mx >0}\\{x + 1 >0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{mx >0}\\{x >- 1}\end{array}} \right.\].

Ta có: $\log \left(mx\right)=2\log (x+1)\iff \log \left(mx\right)=\log {(x+1)}^2$$\iff mx={(x+1)}^2(*)$.

Do $x>-1\iff x+1>0\Rightarrow {(x+1)}^2>0\Rightarrow mx>0$. Do đó $x\ne 0$.

Khi đó ta có $(*)\iff m=\frac{{(x+1)}^2}{x}=f\left(x\right)$, với $x>-1;x\ne 0$.

Ta có:

$f^{\text{'}}\left(x\right)=\frac{2(x+1).x-{(x+1)}^2}{x^2}$

$f^{\text{'}}\left(x\right)=\frac{2x^2+2x-x^2-2x-1}{x^2}$

$f^{\text{'}}\left(x\right)=\frac{x^2-1}{x^2}=0\iff [\begin{array}{l}x=1\\ x=-1\end{array}$

BBT:

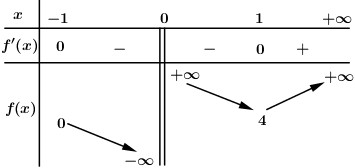
Dựa vào BBT ta thấy phương (*) có nghiệm duy nhất $[\begin{array}{l}m<0\\ m=4\end{array}$.

Kết hợp điều kiện \[m \in \mathbb{Z},{\mkern 1mu} {\mkern 1mu} m \in \left[ { - 2020;2020} \right]\] ta có $m\in \mathbb{Z},m\in [-2020;2020]$.

Vậy có 2021 giá trị của m thỏa mãn yêu cầu bài toán.

Đáp án D.