Cho hình lăng trụ ABC.A'B'C' có thể tích bằng V . Gọi M,N lần lượt là trung điểm của các cạnh AB,A'C'. P là điểm trên cạnh

* Hướng dẫn giải

Phương pháp giải:

- Không mất tính tổng quát, ta giả sử ABC.A'B'C' là lăng trụ đứng để bài toán đơn giản hơn.

- Trong $\left(AC{C}^{\text{'}}{A}^{\text{'}}\right)$ kéo dài NC cắt AA' tại E. Sử dụng tỉ số thể tích Simpson tính $\frac{V_{C.MNP}}{V_{C.MEP}}$.

- Tính $\frac{V_{C.MEP}}{V_{C.AB{B}^{\text{'}}{A}^{\text{'}}}}=\frac{S_{MEP}}{S_{AB{B}^{\text{'}}{A}^{\text{'}}}}$, sử dụng phương pháp phần bù để so sánh $S_{MEP}$với \[{S_{ABB'A'}}\]

- Sử dụng nhận xét $V_{C.AB{B}^{\text{'}}{A}^{\text{'}}}=\frac{2}{3}V$, từ đó tính $V_{CMNP}$ theo V.

Giải chi tiết:

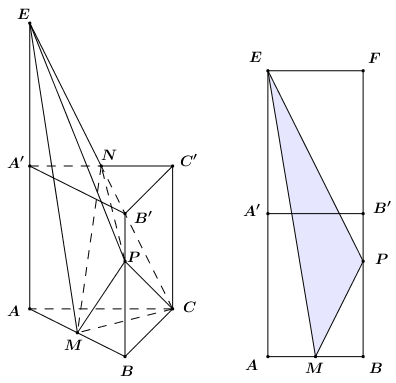
Không mất tính tổng quát, ta giả sử ABC.A'B'C' là lăng trụ đứng để bài toán đơn giản hơn.

Trong (ACC'A') kéo dài NC cắt AA' tại E.

Áp dụng định lí Ta-lét ta có $\frac{A^{\text{'}}N}{AC}=\frac{1}{2}=\frac{E{A}^{\text{'}}}{EA}=\frac{EN}{EC}$$\Rightarrow N$là trung điểm của của CE$\Rightarrow \frac{CN}{CE}=\frac{1}{2}$.

Ta có: $\frac{V_{C.MNP}}{V_{C.MEP}}=\frac{CM}{CM}.\frac{CN}{CE}.\frac{CP}{CP}=\frac{1}{2}\Rightarrow V_{C.MNP}=\frac{1}{2}{V}_{C.MEP}$.

Dựng hình chữ nhật ABFE, ta có:

$S_{ABFE}=S_{AB{B}^{\text{'}}{A}^{\text{'}}}$;

\[\frac{{{S_{EAM}}}}{{{S_{ABFE}}}} = \frac{1}{2}.\frac{{AM}}{{AB}} = \frac{1}{4}\]; $\frac{S_{PEF}}{S_{ABFE}}=\frac{1}{2}.\frac{PF}{BF}=\frac{1}{2}.\frac{2}{3}=\frac{1}{3}$; $\frac{S_{PMB}}{S_{ABFE}}=\frac{1}{2}.\frac{PB}{BF}.\frac{BM}{AB}=\frac{1}{2}.\frac{1}{3}.\frac{1}{2}=\frac{1}{12}$.

Khi đó ta có:

$\begin{array}{l}{S}_{MEP}=S_{ABFE}-S_{EAM}-S_{PEF}-S_{PMB}\\ =S_{ABFE}-\frac{1}{4}{S}_{ABFE}-\frac{1}{3}{S}_{ABFE}-\frac{1}{12}{S}_{ABFE}\\ =\frac{1}{3}{S}_{ABFE}=\frac{2}{3}{S}_{AB{B}^{\text{'}}{A}^{\text{'}}}\end{array}$

Ta có: $\frac{V_{C.MEP}}{V_{C.AB{B}^{\text{'}}{A}^{\text{'}}}}=\frac{S_{MEP}}{S_{AB{B}^{\text{'}}{A}^{\text{'}}}}=\frac{2}{3}$. Mà $V_{C.AB{B}^{\text{'}}{A}^{\text{'}}}=\frac{2}{3}V$nên $V_{C.MEP}=\frac{2}{3}.\frac{2}{3}V=\frac{4}{9}V$.

Vậy $V_{C.MNP}=\frac{1}{2}{V}_{C.MEP}=\frac{2}{9}V$.

Đáp án C.